Sparsity-based Defense against Adversarial Attacks on Linear Classifiers
Paper and Code
Jun 19, 2018

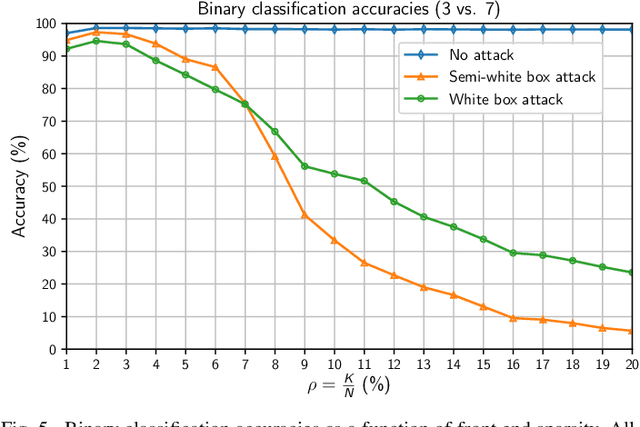
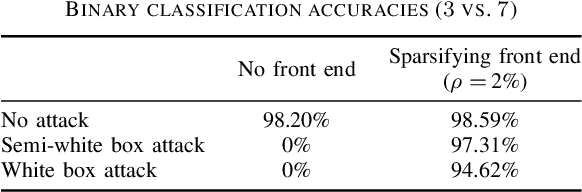
Deep neural networks represent the state of the art in machine learning in a growing number of fields, including vision, speech and natural language processing. However, recent work raises important questions about the robustness of such architectures, by showing that it is possible to induce classification errors through tiny, almost imperceptible, perturbations. Vulnerability to such "adversarial attacks", or "adversarial examples", has been conjectured to be due to the excessive linearity of deep networks. In this paper, we study this phenomenon in the setting of a linear classifier, and show that it is possible to exploit sparsity in natural data to combat $\ell_{\infty}$-bounded adversarial perturbations. Specifically, we demonstrate the efficacy of a sparsifying front end via an ensemble averaged analysis, and experimental results for the MNIST handwritten digit database. To the best of our knowledge, this is the first work to show that sparsity provides a theoretically rigorous framework for defense against adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge