Toward Robust Neural Networks via Sparsification

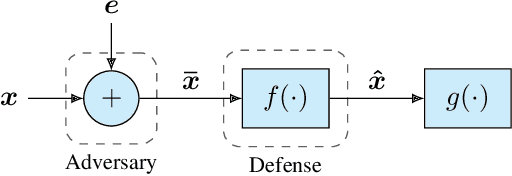
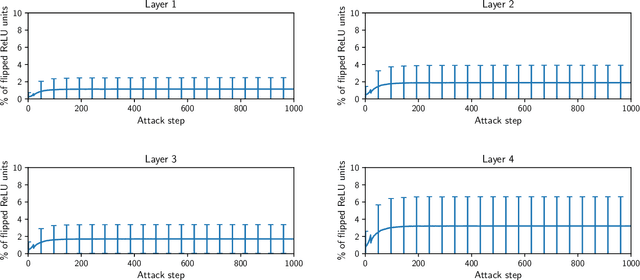
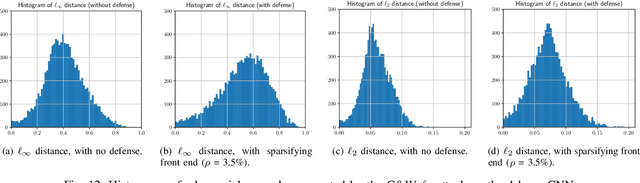
It is by now well-known that small adversarial perturbations can induce classification errors in deep neural networks. In this paper, we make the case that a systematic exploitation of sparsity is key to defending against such attacks, and that a "locally linear" model for neural networks can be used to develop a theoretical foundation for crafting attacks and defenses. We consider two defenses. The first is a sparsifying front end, which attenuates the impact of the attack by a factor of roughly $K/N$ where $N$ is the data dimension and $K$ is the sparsity level. The second is sparsification of network weights, which attenuates the worst-case growth of an attack as it flows up the network. We also devise attacks based on the locally linear model that outperform the well-known FGSM attack. We provide experimental results for the MNIST and Fashion-MNIST datasets, showing the efficacy of the proposed sparsity-based defenses.