On the information in spike timing: neural codes derived from polychronous groups
Paper and Code
Mar 09, 2018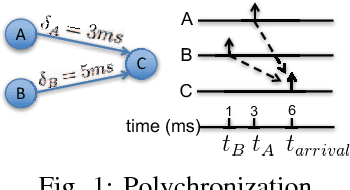
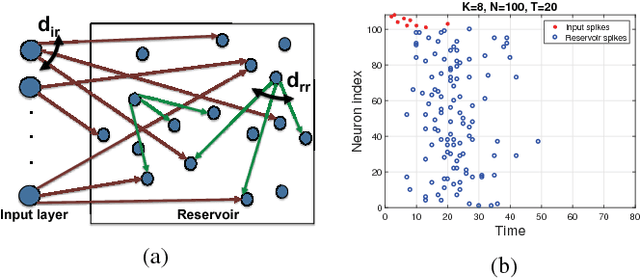
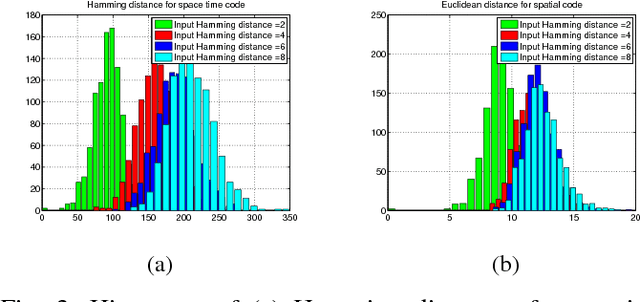
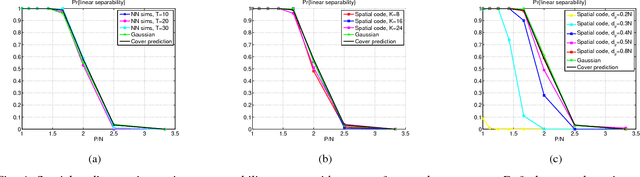
There is growing evidence regarding the importance of spike timing in neural information processing, with even a small number of spikes carrying information, but computational models lag significantly behind those for rate coding. Experimental evidence on neuronal behavior is consistent with the dynamical and state dependent behavior provided by recurrent connections. This motivates the minimalistic abstraction investigated in this paper, aimed at providing insight into information encoding in spike timing via recurrent connections. We employ information-theoretic techniques for a simple reservoir model which encodes input spatiotemporal patterns into a sparse neural code, translating the polychronous groups introduced by Izhikevich into codewords on which we can perform standard vector operations. We show that the distance properties of the code are similar to those for (optimal) random codes. In particular, the code meets benchmarks associated with both linear classification and capacity, with the latter scaling exponentially with reservoir size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge