Simplex Deep Linear Discriminant Analysis

We revisit Deep Linear Discriminant Analysis (Deep LDA) from a likelihood-based perspective. While classical LDA is a simple Gaussian model with linear decision boundaries, attaching an LDA head to a neural encoder raises the question of how to train the resulting deep classifier by maximum likelihood estimation (MLE). We first show that end-to-end MLE training of an unconstrained Deep LDA model ignores discrimination: when both the LDA parameters and the encoder parameters are learned jointly, the likelihood admits a degenerate solution in which some of the class clusters may heavily overlap or even collapse, and classification performance deteriorates. Batchwise moment re-estimation of the LDA parameters does not remove this failure mode. We then propose a constrained Deep LDA formulation that fixes the class means to the vertices of a regular simplex in the latent space and restricts the shared covariance to be spherical, leaving only the priors and a single variance parameter to be learned along with the encoder. Under these geometric constraints, MLE becomes stable and yields well-separated class clusters in the latent space. On images (Fashion-MNIST, CIFAR-10, CIFAR-100), the resulting Deep LDA models achieve accuracy competitive with softmax baselines while offering a simple, interpretable latent geometry that is clearly visible in two-dimensional projections.

Deep Linear Discriminant Analysis Revisited

We show that for unconstrained Deep Linear Discriminant Analysis (LDA) classifiers, maximum-likelihood training admits pathological solutions in which class means drift together, covariances collapse, and the learned representation becomes almost non-discriminative. Conversely, cross-entropy training yields excellent accuracy but decouples the head from the underlying generative model, leading to highly inconsistent parameter estimates. To reconcile generative structure with discriminative performance, we introduce the \emph{Discriminative Negative Log-Likelihood} (DNLL) loss, which augments the LDA log-likelihood with a simple penalty on the mixture density. DNLL can be interpreted as standard LDA NLL plus a term that explicitly discourages regions where several classes are simultaneously likely. Deep LDA trained with DNLL produces clean, well-separated latent spaces, matches the test accuracy of softmax classifiers on synthetic data and standard image benchmarks, and yields substantially better calibrated predictive probabilities, restoring a coherent probabilistic interpretation to deep discriminant models.

Overspecified Mixture Discriminant Analysis: Exponential Convergence, Statistical Guarantees, and Remote Sensing Applications

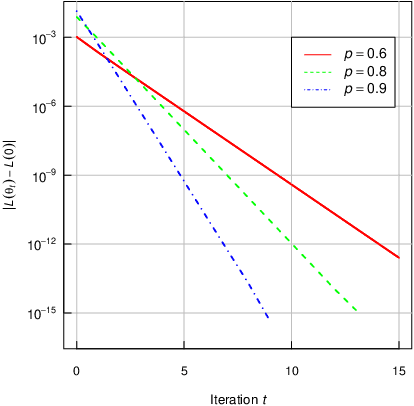
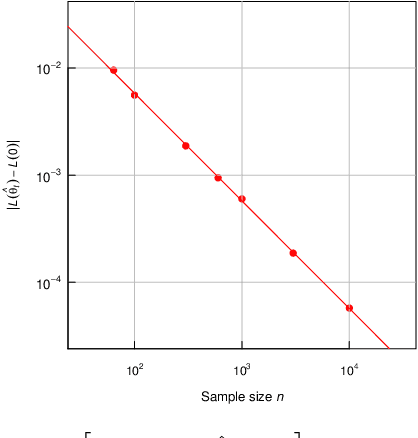
This study explores the classification error of Mixture Discriminant Analysis (MDA) in scenarios where the number of mixture components exceeds those present in the actual data distribution, a condition known as overspecification. We use a two-component Gaussian mixture model within each class to fit data generated from a single Gaussian, analyzing both the algorithmic convergence of the Expectation-Maximization (EM) algorithm and the statistical classification error. We demonstrate that, with suitable initialization, the EM algorithm converges exponentially fast to the Bayes risk at the population level. Further, we extend our results to finite samples, showing that the classification error converges to Bayes risk with a rate $n^{-1/2}$ under mild conditions on the initial parameter estimates and sample size. This work provides a rigorous theoretical framework for understanding the performance of overspecified MDA, which is often used empirically in complex data settings, such as image and text classification. To validate our theory, we conduct experiments on remote sensing datasets.

Learning Overspecified Gaussian Mixtures Exponentially Fast with the EM Algorithm

We investigate the convergence properties of the EM algorithm when applied to overspecified Gaussian mixture models -- that is, when the number of components in the fitted model exceeds that of the true underlying distribution. Focusing on a structured configuration where the component means are positioned at the vertices of a regular simplex and the mixture weights satisfy a non-degeneracy condition, we demonstrate that the population EM algorithm converges exponentially fast in terms of the Kullback-Leibler (KL) distance. Our analysis leverages the strong convexity of the negative log-likelihood function in a neighborhood around the optimum and utilizes the Polyak-{\L}ojasiewicz inequality to establish that an $\epsilon$-accurate approximation is achievable in $O(\log(1/\epsilon))$ iterations. Furthermore, we extend these results to a finite-sample setting by deriving explicit statistical convergence guarantees. Numerical experiments on synthetic datasets corroborate our theoretical findings, highlighting the dramatic acceleration in convergence compared to conventional sublinear rates. This work not only deepens the understanding of EM's behavior in overspecified settings but also offers practical insights into initialization strategies and model design for high-dimensional clustering and density estimation tasks.

Gradient Descent Fails to Learn High-frequency Functions and Modular Arithmetic

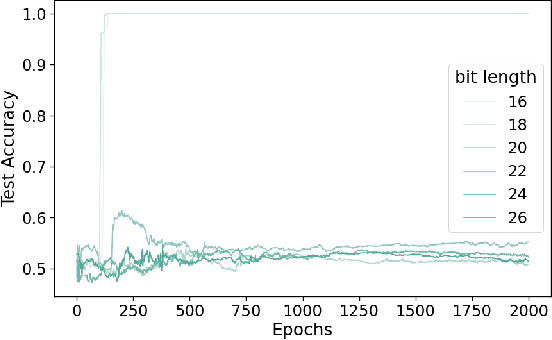
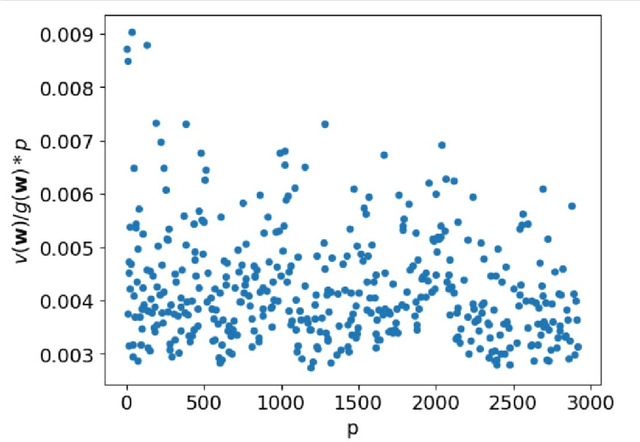
Classes of target functions containing a large number of approximately orthogonal elements are known to be hard to learn by the Statistical Query algorithms. Recently this classical fact re-emerged in a theory of gradient-based optimization of neural networks. In the novel framework, the hardness of a class is usually quantified by the variance of the gradient with respect to a random choice of a target function. A set of functions of the form $x\to ax \bmod p$, where $a$ is taken from ${\mathbb Z}_p$, has attracted some attention from deep learning theorists and cryptographers recently. This class can be understood as a subset of $p$-periodic functions on ${\mathbb Z}$ and is tightly connected with a class of high-frequency periodic functions on the real line. We present a mathematical analysis of limitations and challenges associated with using gradient-based learning techniques to train a high-frequency periodic function or modular multiplication from examples. We highlight that the variance of the gradient is negligibly small in both cases when either a frequency or the prime base $p$ is large. This in turn prevents such a learning algorithm from being successful.

Intractability of Learning the Discrete Logarithm with Gradient-Based Methods

The discrete logarithm problem is a fundamental challenge in number theory with significant implications for cryptographic protocols. In this paper, we investigate the limitations of gradient-based methods for learning the parity bit of the discrete logarithm in finite cyclic groups of prime order. Our main result, supported by theoretical analysis and empirical verification, reveals the concentration of the gradient of the loss function around a fixed point, independent of the logarithm's base used. This concentration property leads to a restricted ability to learn the parity bit efficiently using gradient-based methods, irrespective of the complexity of the network architecture being trained. Our proof relies on Boas-Bellman inequality in inner product spaces and it involves establishing approximate orthogonality of discrete logarithm's parity bit functions through the spectral norm of certain matrices. Empirical experiments using a neural network-based approach further verify the limitations of gradient-based learning, demonstrating the decreasing success rate in predicting the parity bit as the group order increases.

Long-Tail Theory under Gaussian Mixtures

We suggest a simple Gaussian mixture model for data generation that complies with Feldman's long tail theory (2020). We demonstrate that a linear classifier cannot decrease the generalization error below a certain level in the proposed model, whereas a nonlinear classifier with a memorization capacity can. This confirms that for long-tailed distributions, rare training examples must be considered for optimal generalization to new data. Finally, we show that the performance gap between linear and nonlinear models can be lessened as the tail becomes shorter in the subpopulation frequency distribution, as confirmed by experiments on synthetic and real data.

From Hyperbolic Geometry Back to Word Embeddings

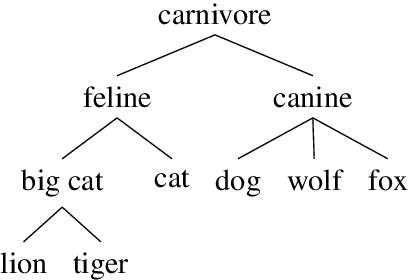
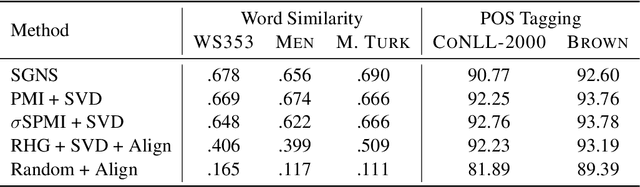
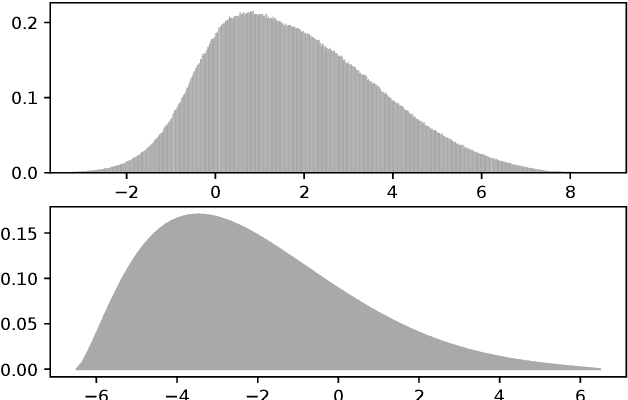
We choose random points in the hyperbolic disc and claim that these points are already word representations. However, it is yet to be uncovered which point corresponds to which word of the human language of interest. This correspondence can be approximately established using a pointwise mutual information between words and recent alignment techniques.

Speeding Up Entmax

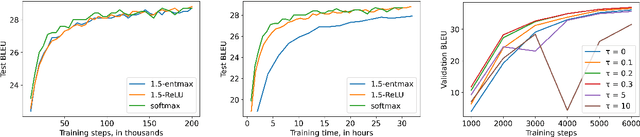
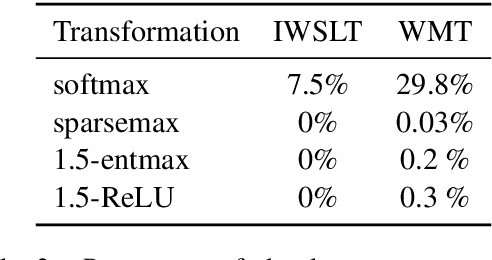
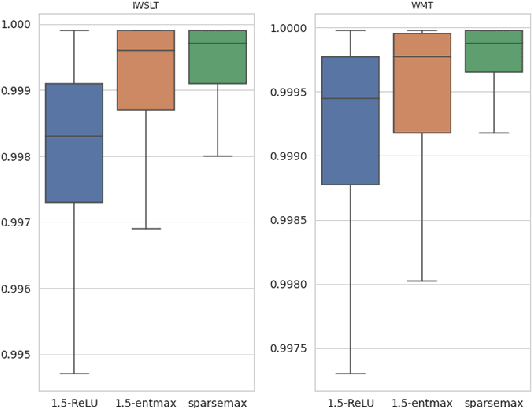
Softmax is the de facto standard in modern neural networks for language processing when it comes to normalizing logits. However, by producing a dense probability distribution each token in the vocabulary has a nonzero chance of being selected at each generation step, leading to a variety of reported problems in text generation. $\alpha$-entmax of Peters et al. (2019, arXiv:1905.05702) solves this problem, but is considerably slower than softmax. In this paper, we propose an alternative to $\alpha$-entmax, which keeps its virtuous characteristics, but is as fast as optimized softmax and achieves on par or better performance in machine translation task.

The Rediscovery Hypothesis: Language Models Need to Meet Linguistics

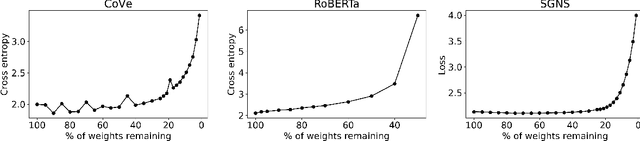
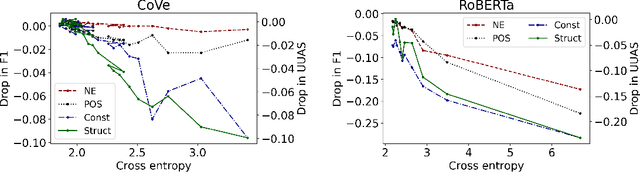
There is an ongoing debate in the NLP community whether modern language models contain linguistic knowledge, recovered through so-called \textit{probes}. In this paper we study whether linguistic knowledge is a necessary condition for good performance of modern language models, which we call the \textit{rediscovery hypothesis}. In the first place we show that language models that are significantly compressed but perform well on their pretraining objectives retain good scores when probed for linguistic structures. This result supports the rediscovery hypothesis and leads to the second contribution of our paper: an information-theoretic framework that relates language modeling objective with linguistic information. This framework also provides a metric to measure the impact of linguistic information on the word prediction task. We reinforce our analytical results with various experiments, both on synthetic and on real tasks.