Spectral Algorithms under Covariate Shift

Spectral algorithms leverage spectral regularization techniques to analyze and process data, providing a flexible framework for addressing supervised learning problems. To deepen our understanding of their performance in real-world scenarios where the distributions of training and test data may differ, we conduct a rigorous investigation into the convergence behavior of spectral algorithms under distribution shifts, specifically within the framework of reproducing kernel Hilbert spaces. Our study focuses on the case of covariate shift. In this scenario, the marginal distributions of the input data differ between the training and test datasets, while the conditional distribution of the output given the input remains unchanged. Under this setting, we analyze the generalization error of spectral algorithms and show that they achieve minimax optimality when the density ratios between the training and test distributions are uniformly bounded. However, we also identify a critical limitation: when the density ratios are unbounded, the spectral algorithms may become suboptimal. To address this limitation, we propose a weighted spectral algorithm that incorporates density ratio information into the learning process. Our theoretical analysis shows that this weighted approach achieves optimal capacity-independent convergence rates. Furthermore, by introducing a weight clipping technique, we demonstrate that the convergence rates of the weighted spectral algorithm can approach the optimal capacity-dependent convergence rates arbitrarily closely. This improvement resolves the suboptimality issue in unbounded density ratio scenarios and advances the state-of-the-art by refining existing theoretical results.

Stochastic Gradient Descent for Two-layer Neural Networks

This paper presents a comprehensive study on the convergence rates of the stochastic gradient descent (SGD) algorithm when applied to overparameterized two-layer neural networks. Our approach combines the Neural Tangent Kernel (NTK) approximation with convergence analysis in the Reproducing Kernel Hilbert Space (RKHS) generated by NTK, aiming to provide a deep understanding of the convergence behavior of SGD in overparameterized two-layer neural networks. Our research framework enables us to explore the intricate interplay between kernel methods and optimization processes, shedding light on the optimization dynamics and convergence properties of neural networks. In this study, we establish sharp convergence rates for the last iterate of the SGD algorithm in overparameterized two-layer neural networks. Additionally, we have made significant advancements in relaxing the constraints on the number of neurons, which have been reduced from exponential dependence to polynomial dependence on the sample size or number of iterations. This improvement allows for more flexibility in the design and scaling of neural networks, and will deepen our theoretical understanding of neural network models trained with SGD.

Optimality of Robust Online Learning

In this paper, we study an online learning algorithm with a robust loss function $\mathcal{L}_{\sigma}$ for regression over a reproducing kernel Hilbert space (RKHS). The loss function $\mathcal{L}_{\sigma}$ involving a scaling parameter $\sigma>0$ can cover a wide range of commonly used robust losses. The proposed algorithm is then a robust alternative for online least squares regression aiming to estimate the conditional mean function. For properly chosen $\sigma$ and step size, we show that the last iterate of this online algorithm can achieve optimal capacity independent convergence in the mean square distance. Moreover, if additional information on the underlying function space is known, we also establish optimal capacity dependent rates for strong convergence in RKHS. To the best of our knowledge, both of the two results are new to the existing literature of online learning.

Online Regularized Learning Algorithm for Functional Data

In recent years, functional linear models have attracted growing attention in statistics and machine learning, with the aim of recovering the slope function or its functional predictor. This paper considers online regularized learning algorithm for functional linear models in reproducing kernel Hilbert spaces. Convergence analysis of excess prediction error and estimation error are provided with polynomially decaying step-size and constant step-size, respectively. Fast convergence rates can be derived via a capacity dependent analysis. By introducing an explicit regularization term, we uplift the saturation boundary of unregularized online learning algorithms when the step-size decays polynomially, and establish fast convergence rates of estimation error without capacity assumption. However, it remains an open problem to obtain capacity independent convergence rates for the estimation error of the unregularized online learning algorithm with decaying step-size. It also shows that convergence rates of both prediction error and estimation error with constant step-size are competitive with those in the literature.

Capacity dependent analysis for functional online learning algorithms

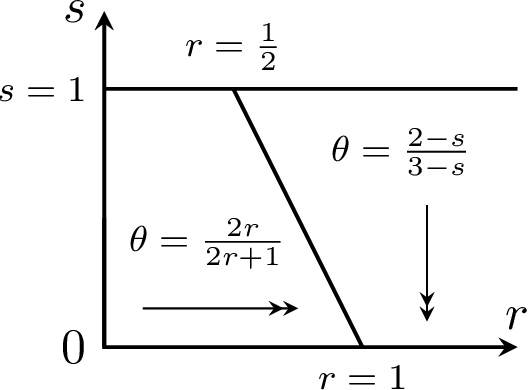
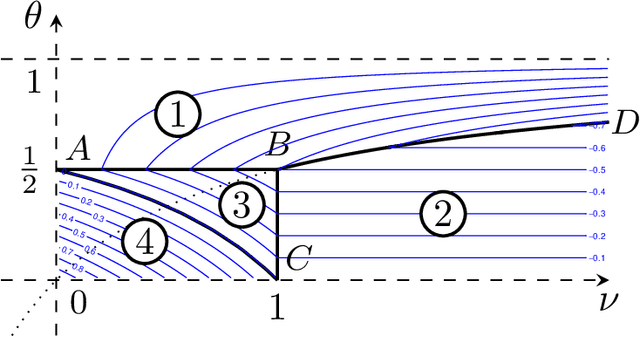
This article provides convergence analysis of online stochastic gradient descent algorithms for functional linear models. Adopting the characterizations of the slope function regularity, the kernel space capacity, and the capacity of the sampling process covariance operator, significant improvement on the convergence rates is achieved. Both prediction problems and estimation problems are studied, where we show that capacity assumption can alleviate the saturation of the convergence rate as the regularity of the target function increases. We show that with properly selected kernel, capacity assumptions can fully compensate for the regularity assumptions for prediction problems (but not for estimation problems). This demonstrates the significant difference between the prediction problems and the estimation problems in functional data analysis.

Coefficient-based Regularized Distribution Regression

In this paper, we consider the coefficient-based regularized distribution regression which aims to regress from probability measures to real-valued responses over a reproducing kernel Hilbert space (RKHS), where the regularization is put on the coefficients and kernels are assumed to be indefinite. The algorithm involves two stages of sampling, the first stage sample consists of distributions and the second stage sample is obtained from these distributions. Asymptotic behaviors of the algorithm in different regularity ranges of the regression function are comprehensively studied and learning rates are derived via integral operator techniques. We get the optimal rates under some mild conditions, which matches the one-stage sampled minimax optimal rate. Compared with the kernel methods for distribution regression in the literature, the algorithm under consideration does not require the kernel to be symmetric and positive semi-definite and hence provides a simple paradigm for designing indefinite kernel methods, which enriches the theme of the distribution regression. To the best of our knowledge, this is the first result for distribution regression with indefinite kernels, and our algorithm can improve the saturation effect.

Realizing data features by deep nets

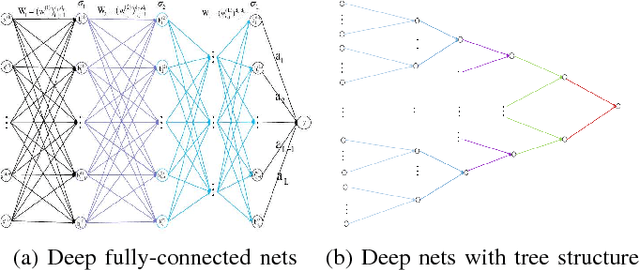
This paper considers the power of deep neural networks (deep nets for short) in realizing data features. Based on refined covering number estimates, we find that, to realize some complex data features, deep nets can improve the performances of shallow neural networks (shallow nets for short) without requiring additional capacity costs. This verifies the advantage of deep nets in realizing complex features. On the other hand, to realize some simple data feature like the smoothness, we prove that, up to a logarithmic factor, the approximation rate of deep nets is asymptotically identical to that of shallow nets, provided that the depth is fixed. This exhibits a limitation of deep nets in realizing simple features.

Fast and Strong Convergence of Online Learning Algorithms

In this paper, we study the online learning algorithm without explicit regularization terms. This algorithm is essentially a stochastic gradient descent scheme in a reproducing kernel Hilbert space (RKHS). The polynomially decaying step size in each iteration can play a role of regularization to ensure the generalization ability of online learning algorithm. We develop a novel capacity dependent analysis on the performance of the last iterate of online learning algorithm. The contribution of this paper is two-fold. First, our nice analysis can lead to the convergence rate in the standard mean square distance which is the best so far. Second, we establish, for the first time, the strong convergence of the last iterate with polynomially decaying step sizes in the RKHS norm. We demonstrate that the theoretical analysis established in this paper fully exploits the fine structure of the underlying RKHS, and thus can lead to sharp error estimates of online learning algorithm.

Convergence of Unregularized Online Learning Algorithms

In this paper we study the convergence of online gradient descent algorithms in reproducing kernel Hilbert spaces (RKHSs) without regularization. We establish a sufficient condition and a necessary condition for the convergence of excess generalization errors in expectation. A sufficient condition for the almost sure convergence is also given. With high probability, we provide explicit convergence rates of the excess generalization errors for both averaged iterates and the last iterate, which in turn also imply convergence rates with probability one. To our best knowledge, this is the first high-probability convergence rate for the last iterate of online gradient descent algorithms without strong convexity. Without any boundedness assumptions on iterates, our results are derived by a novel use of two measures of the algorithm's one-step progress, respectively by generalization errors and by distances in RKHSs, where the variances of the involved martingales are cancelled out by the descent property of the algorithm.

Learning from networked examples

Many machine learning algorithms are based on the assumption that training examples are drawn independently. However, this assumption does not hold anymore when learning from a networked sample because two or more training examples may share some common objects, and hence share the features of these shared objects. We show that the classic approach of ignoring this problem potentially can have a harmful effect on the accuracy of statistics, and then consider alternatives. One of these is to only use independent examples, discarding other information. However, this is clearly suboptimal. We analyze sample error bounds in this networked setting, providing significantly improved results. An important component of our approach is formed by efficient sample weighting schemes, which leads to novel concentration inequalities.