Capacity dependent analysis for functional online learning algorithms
Paper and Code
Sep 25, 2022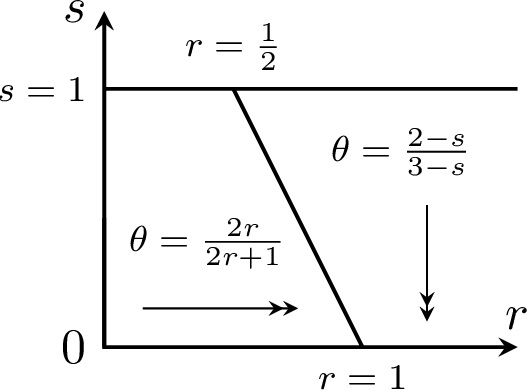
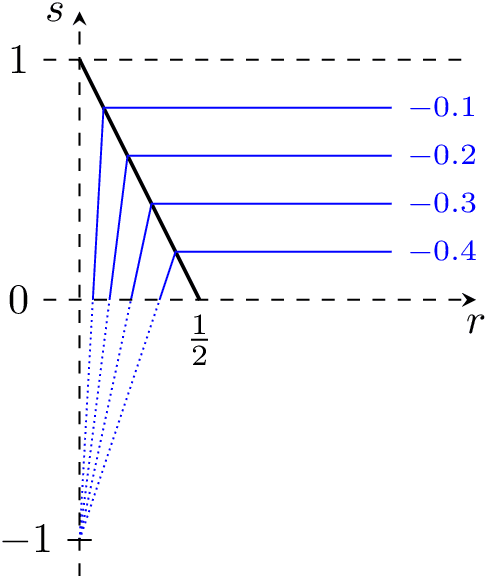
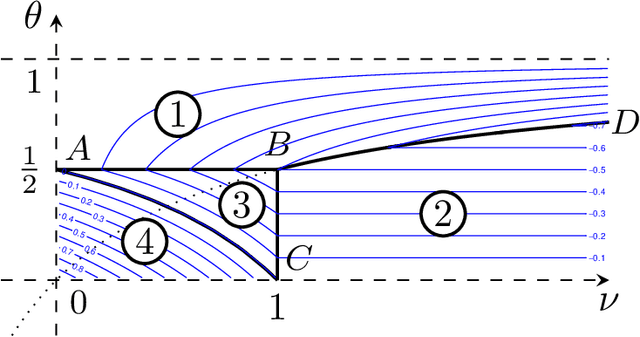
This article provides convergence analysis of online stochastic gradient descent algorithms for functional linear models. Adopting the characterizations of the slope function regularity, the kernel space capacity, and the capacity of the sampling process covariance operator, significant improvement on the convergence rates is achieved. Both prediction problems and estimation problems are studied, where we show that capacity assumption can alleviate the saturation of the convergence rate as the regularity of the target function increases. We show that with properly selected kernel, capacity assumptions can fully compensate for the regularity assumptions for prediction problems (but not for estimation problems). This demonstrates the significant difference between the prediction problems and the estimation problems in functional data analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge