Ascend HiFloat8 Format for Deep Learning

This preliminary white paper proposes a novel 8-bit floating-point data format HiFloat8 (abbreviated as HiF8) for deep learning. HiF8 features tapered precision. For normal value encoding, it provides 7 exponent values with 3-bit mantissa, 8 exponent values with 2-bit mantissa, and 16 exponent values with 1-bit mantissa. For denormal value encoding, it extends the dynamic range by 7 extra powers of 2, from 31 to 38 binades (notice that FP16 covers 40 binades). Meanwhile, HiF8 encodes all the special values except that positive zero and negative zero are represented by only one bit-pattern. Thanks to the better balance between precision and dynamic range, HiF8 can be simultaneously used in both forward and backward passes of AI training. In this paper, we will describe the definition and rounding methods of HiF8, as well as the tentative training and inference solutions. To demonstrate the efficacy of HiF8, massive simulation results on various neural networks, including traditional neural networks and large language models (LLMs), will also be presented.

Relational Multi-Manifold Co-Clustering

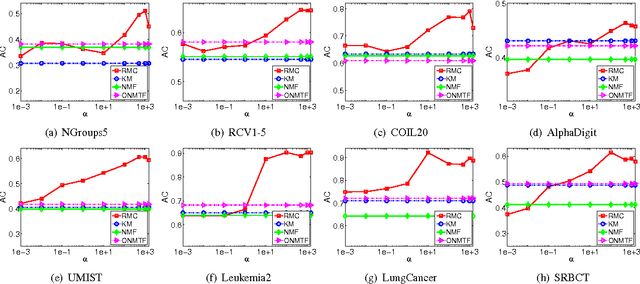
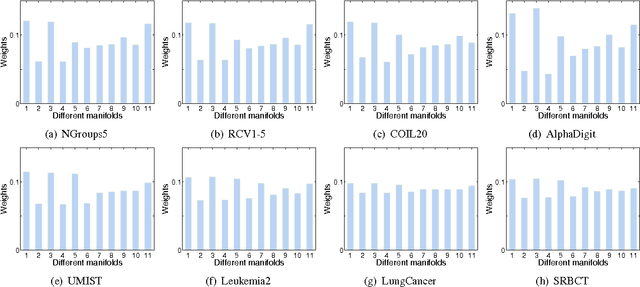
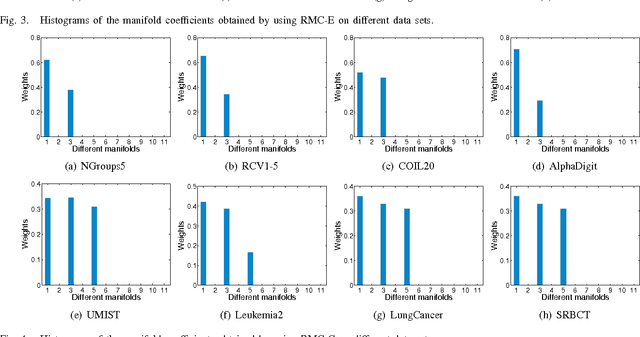
Co-clustering targets on grouping the samples (e.g., documents, users) and the features (e.g., words, ratings) simultaneously. It employs the dual relation and the bilateral information between the samples and features. In many realworld applications, data usually reside on a submanifold of the ambient Euclidean space, but it is nontrivial to estimate the intrinsic manifold of the data space in a principled way. In this study, we focus on improving the co-clustering performance via manifold ensemble learning, which is able to maximally approximate the intrinsic manifolds of both the sample and feature spaces. To achieve this, we develop a novel co-clustering algorithm called Relational Multi-manifold Co-clustering (RMC) based on symmetric nonnegative matrix tri-factorization, which decomposes the relational data matrix into three submatrices. This method considers the intertype relationship revealed by the relational data matrix, and also the intra-type information reflected by the affinity matrices encoded on the sample and feature data distributions. Specifically, we assume the intrinsic manifold of the sample or feature space lies in a convex hull of some pre-defined candidate manifolds. We want to learn a convex combination of them to maximally approach the desired intrinsic manifold. To optimize the objective function, the multiplicative rules are utilized to update the submatrices alternatively. Besides, both the entropic mirror descent algorithm and the coordinate descent algorithm are exploited to learn the manifold coefficient vector. Extensive experiments on documents, images and gene expression data sets have demonstrated the superiority of the proposed algorithm compared to other well-established methods.