VS-TransGRU: A Novel Transformer-GRU-based Framework Enhanced by Visual-Semantic Fusion for Egocentric Action Anticipation

Egocentric action anticipation is a challenging task that aims to make advanced predictions of future actions from current and historical observations in the first-person view. Most existing methods focus on improving the model architecture and loss function based on the visual input and recurrent neural network to boost the anticipation performance. However, these methods, which merely consider visual information and rely on a single network architecture, gradually reach a performance plateau. In order to fully understand what has been observed and capture the dependencies between current observations and future actions well enough, we propose a novel visual-semantic fusion enhanced and Transformer GRU-based action anticipation framework in this paper. Firstly, high-level semantic information is introduced to improve the performance of action anticipation for the first time. We propose to use the semantic features generated based on the class labels or directly from the visual observations to augment the original visual features. Secondly, an effective visual-semantic fusion module is proposed to make up for the semantic gap and fully utilize the complementarity of different modalities. Thirdly, to take advantage of both the parallel and autoregressive models, we design a Transformer based encoder for long-term sequential modeling and a GRU-based decoder for flexible iteration decoding. Extensive experiments on two large-scale first-person view datasets, i.e., EPIC-Kitchens and EGTEA Gaze+, validate the effectiveness of our proposed method, which achieves new state-of-the-art performance, outperforming previous approaches by a large margin.

Solving Poisson's Equation using Deep Learning in Particle Simulation of PN Junction

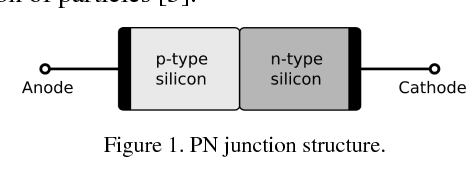
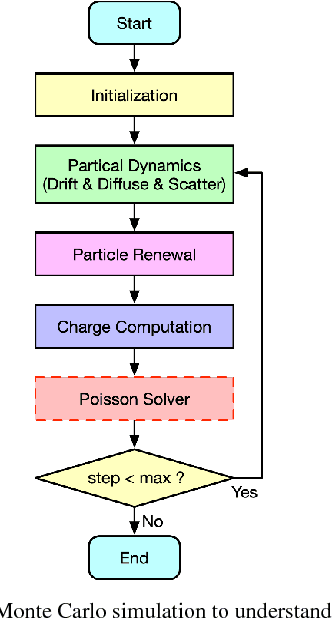
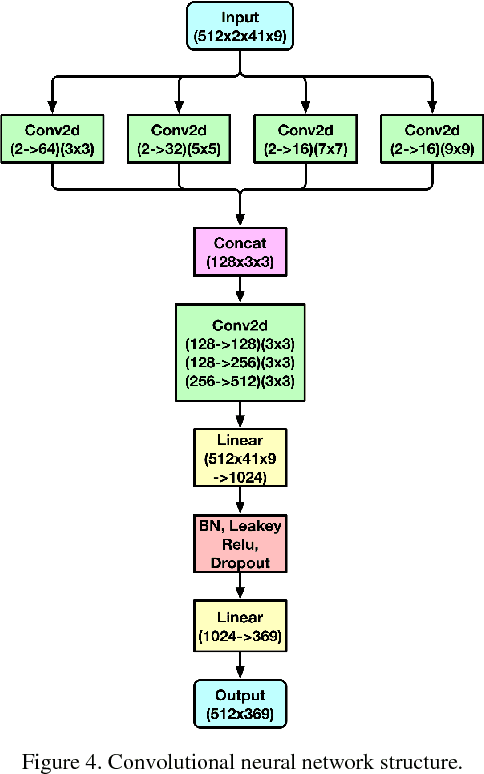
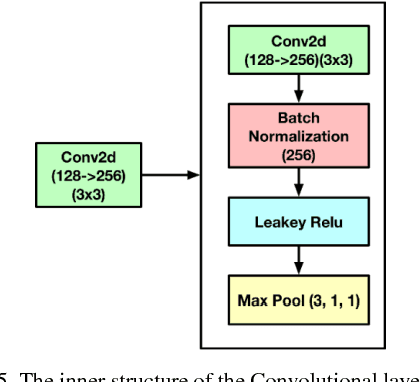
Simulating the dynamic characteristics of a PN junction at the microscopic level requires solving the Poisson's equation at every time step. Solving at every time step is a necessary but time-consuming process when using the traditional finite difference (FDM) approach. Deep learning is a powerful technique to fit complex functions. In this work, deep learning is utilized to accelerate solving Poisson's equation in a PN junction. The role of the boundary condition is emphasized in the loss function to ensure a better fitting. The resulting I-V curve for the PN junction, using the deep learning solver presented in this work, shows a perfect match to the I-V curve obtained using the finite difference method, with the advantage of being 10 times faster at every time step.