Nicholas Erickson
Missouri S&T EMC Laboratory, Rolla, MO, USA
Solving Poisson's Equation using Deep Learning in Particle Simulation of PN Junction
Oct 25, 2018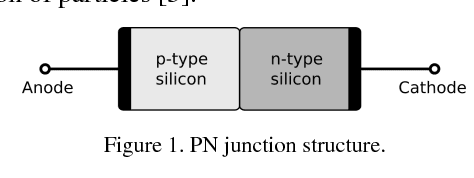
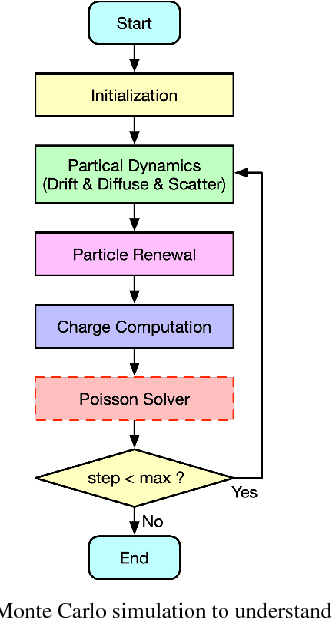
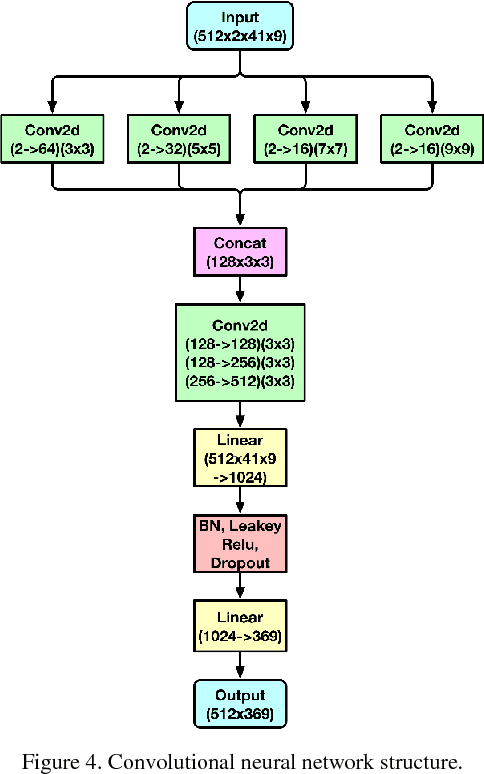
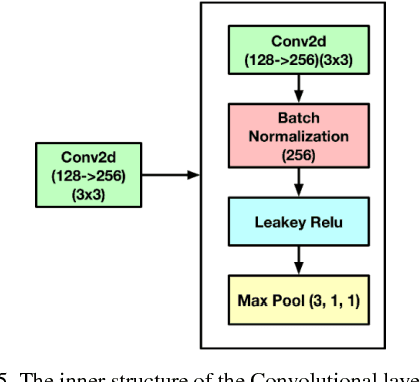
Abstract:Simulating the dynamic characteristics of a PN junction at the microscopic level requires solving the Poisson's equation at every time step. Solving at every time step is a necessary but time-consuming process when using the traditional finite difference (FDM) approach. Deep learning is a powerful technique to fit complex functions. In this work, deep learning is utilized to accelerate solving Poisson's equation in a PN junction. The role of the boundary condition is emphasized in the loss function to ensure a better fitting. The resulting I-V curve for the PN junction, using the deep learning solver presented in this work, shows a perfect match to the I-V curve obtained using the finite difference method, with the advantage of being 10 times faster at every time step.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge