Adaptation to Misspecified Kernel Regularity in Kernelised Bandits

In continuum-armed bandit problems where the underlying function resides in a reproducing kernel Hilbert space (RKHS), namely, the kernelised bandit problems, an important open problem remains of how well learning algorithms can adapt if the regularity of the associated kernel function is unknown. In this work, we study adaptivity to the regularity of translation-invariant kernels, which is characterized by the decay rate of the Fourier transformation of the kernel, in the bandit setting. We derive an adaptivity lower bound, proving that it is impossible to simultaneously achieve optimal cumulative regret in a pair of RKHSs with different regularities. To verify the tightness of this lower bound, we show that an existing bandit model selection algorithm applied with minimax non-adaptive kernelised bandit algorithms matches the lower bound in dependence of $T$, the total number of steps, except for log factors. By filling in the regret bounds for adaptivity between RKHSs, we connect the statistical difficulty for adaptivity in continuum-armed bandits in three fundamental types of function spaces: RKHS, Sobolev space, and H\"older space.

Integrating Rankings into Quantized Scores in Peer Review

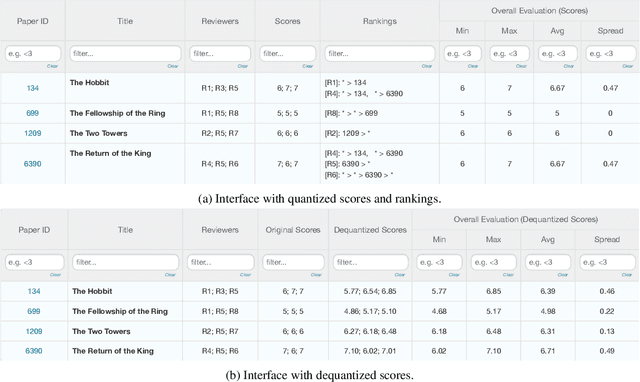
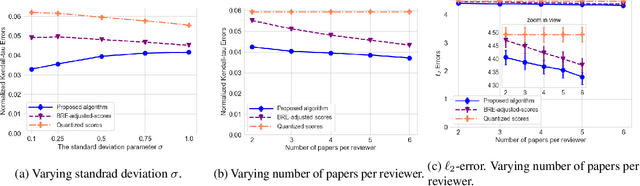
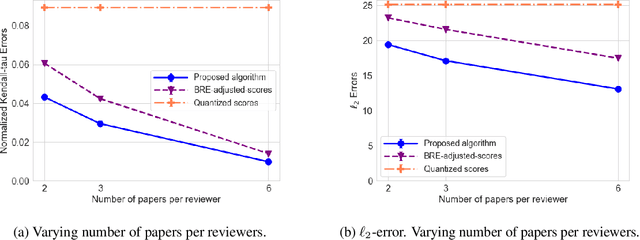
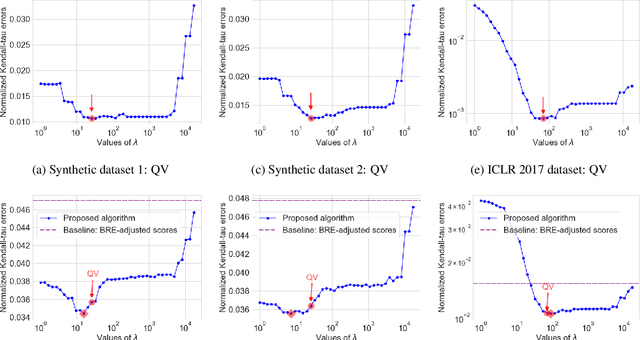
In peer review, reviewers are usually asked to provide scores for the papers. The scores are then used by Area Chairs or Program Chairs in various ways in the decision-making process. The scores are usually elicited in a quantized form to accommodate the limited cognitive ability of humans to describe their opinions in numerical values. It has been found that the quantized scores suffer from a large number of ties, thereby leading to a significant loss of information. To mitigate this issue, conferences have started to ask reviewers to additionally provide a ranking of the papers they have reviewed. There are however two key challenges. First, there is no standard procedure for using this ranking information and Area Chairs may use it in different ways (including simply ignoring them), thereby leading to arbitrariness in the peer-review process. Second, there are no suitable interfaces for judicious use of this data nor methods to incorporate it in existing workflows, thereby leading to inefficiencies. We take a principled approach to integrate the ranking information into the scores. The output of our method is an updated score pertaining to each review that also incorporates the rankings. Our approach addresses the two aforementioned challenges by: (i) ensuring that rankings are incorporated into the updates scores in the same manner for all papers, thereby mitigating arbitrariness, and (ii) allowing to seamlessly use existing interfaces and workflows designed for scores. We empirically evaluate our method on synthetic datasets as well as on peer reviews from the ICLR 2017 conference, and find that it reduces the error by approximately 30% as compared to the best performing baseline on the ICLR 2017 data.

Low-Complexity Improved-Throughput Generalised Spatial Modulation: Bit-to-Symbol Mapping, Detection and Performance Analysis

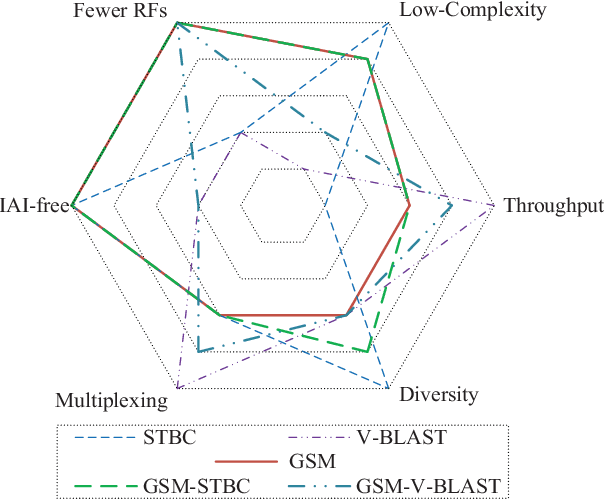
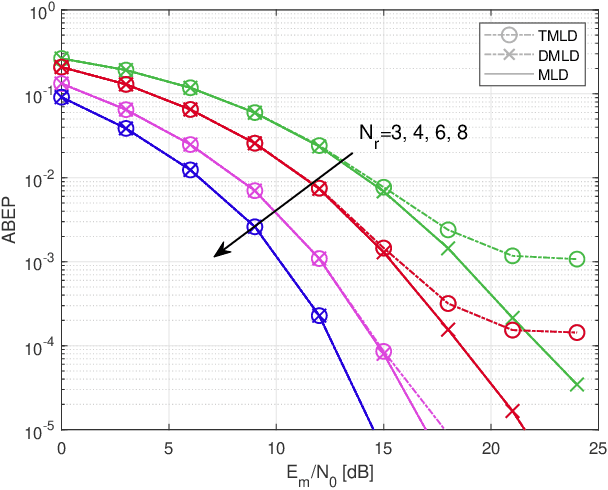
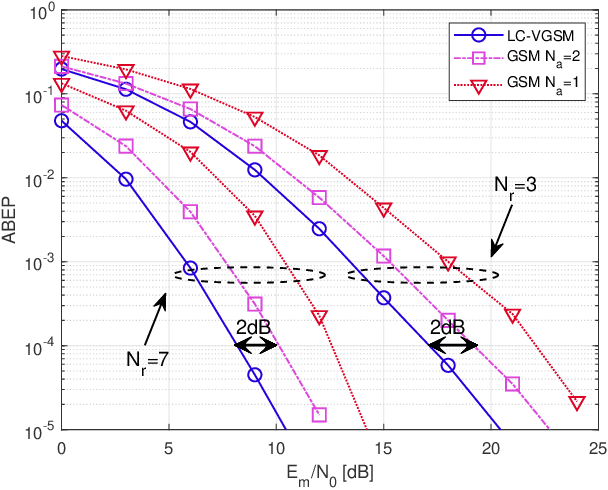
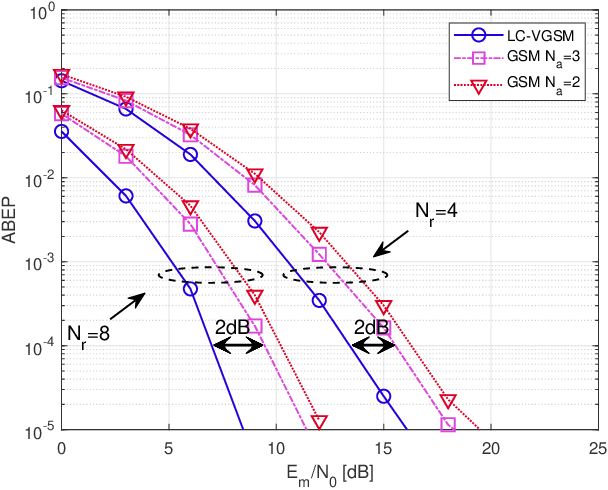
Low-complexity improved-throughput generalised spatial modulation (LCIT-GSM) is proposed. More explicitly, in GSM, extra information bits are conveyed implicitly by activating a fixed number $N_{a}$ out of $N_{t}$ transmit antennas (TAs) at a time. As a result, GSM has the advantage of a reduced number of radio-frequency (RF) chains and reduced inter-antenna interference (IAI) at the cost of a lower throughput than its multiplexing-oriented full-RF based counterparts. Variable-${N_a}$ GSM mitigates this throughput reduction by incorporating all possible TA activation patterns associated with a variable value $N_{a}$ ranging from $1$ to $N_{t}$ during a single channel-use, which maximises the throughput of GSM but suffers a high complexity of the mapping book design and demodulation. In order to mitigate the complexity, \emph{first of all}, we propose two efficient schemes for mapping the information bits to the TA activation patterns, which can be readily scaled to massive MIMO setups. \emph{Secondly}, in the absence of IAI, we derive a pair of low-complexity near-optimal detectors, one of them has a reduced search scope, while the other benefits from a decoupled single-stream based signal detection algorithm. \emph{Finally}, the performance of the proposed LCIT-GSM system is characterised by the error probability upper bound (UB). Our Monte Carlo based simulation results confirm the improved error performance of our proposed scheme, despite its reduced signal detection complexity.

Joint Training of the Superimposed Direct and Reflected Links in Reconfigurable Intelligent Surface Assisted Multiuser Communications

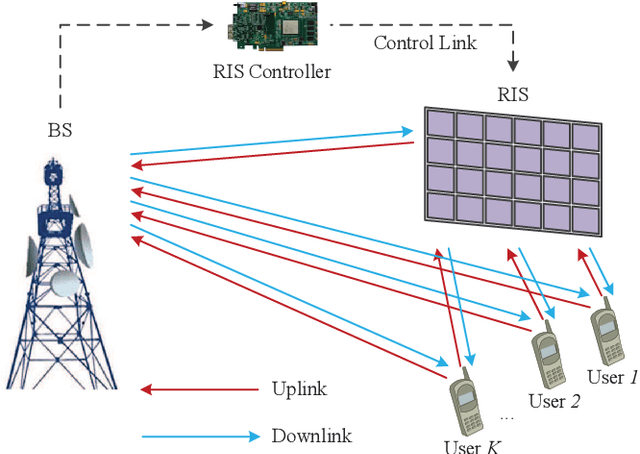
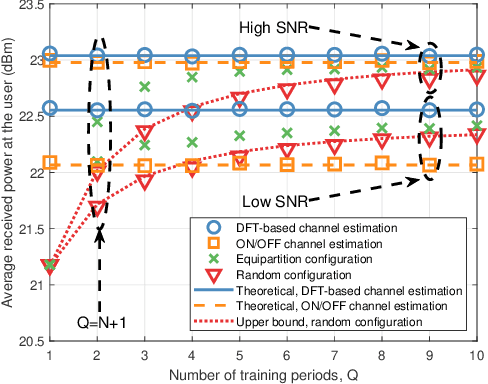
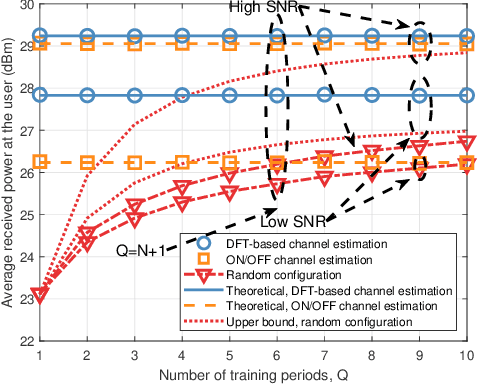
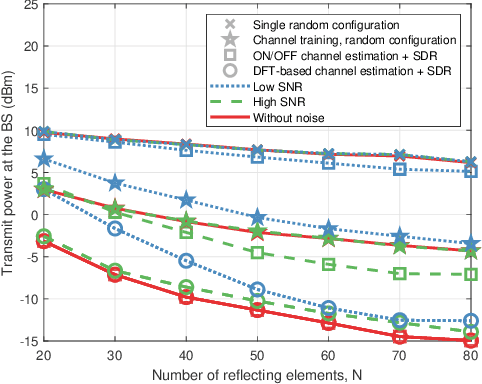
In Reconfigurable intelligent surface (RIS)-assisted systems the acquisition of CSI and the optimization of the reflecting coefficients constitute a pair of salient design issues. In this paper, a novel channel training protocol is proposed, which is capable of achieving a flexible performance vs. signalling and pilot overhead as well as implementation complexity trade-off. More specifically, first of all, we conceive a holistic channel estimation protocol, which integrates the existing channel estimation techniques and passive beamforming design. Secondly, we propose a new channel training framework. In contrast to the conventional channel estimation arrangements, our new framework divides the training phase into several periods, where the superimposed end-to-end channel is estimated instead of separately estimating the direct BS-user channel and cascaded reflected BS-RIS-user channels. As a result, the reflecting coefficients of the RIS are optimized by comparing the objective function values over multiple training periods. Moreover, the theoretical performance of our channel training protocol is analyzed and compared to that under the optimal reflecting coefficients. In addition, the potential benefits of our channel training protocol in reducing the complexity, pilot overhead as well as signalling overhead are also detailed. Thirdly, we derive the theoretical performance of channel estimation protocols and our channel training protocol in the presence of noise for a SISO scenario, which provides useful insights into the impact of the noise on the overall RIS performance. Finally, our numerical simulations characterize the performance of the proposed protocols and verify our theoretical analysis. In particular, the simulation results demonstrate that our channel training protocol is more competitive than the channel estimation protocol at low signal-to-noise ratios.

HyperRNN: Deep Learning-Aided Downlink CSI Acquisition via Partial Channel Reciprocity for FDD Massive MIMO

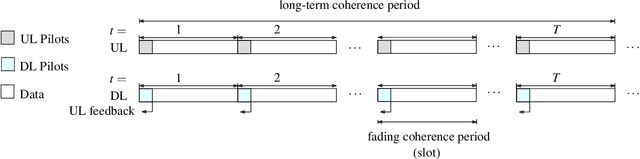
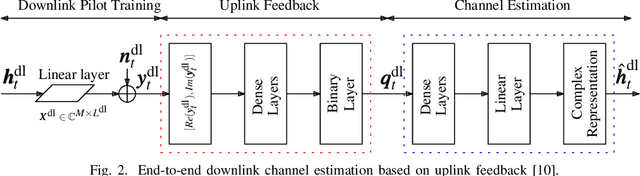
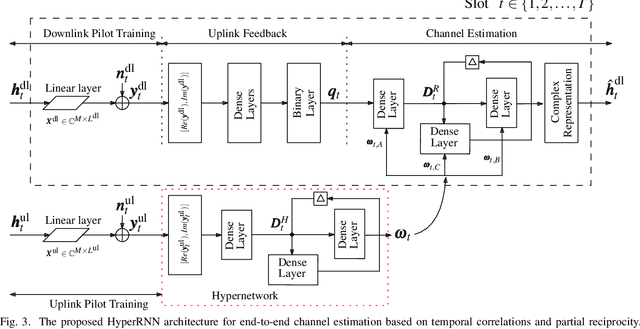
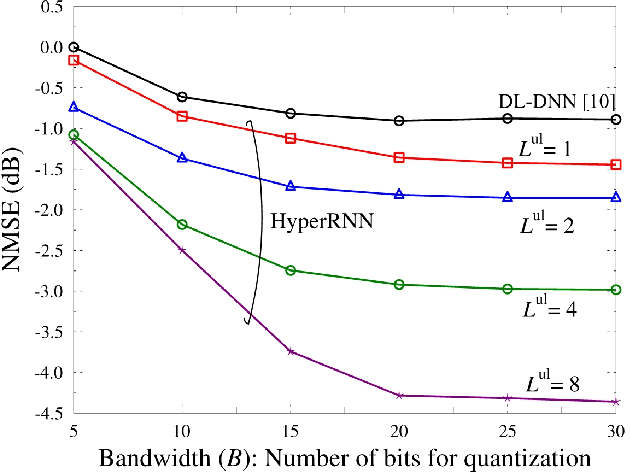
In order to unlock the full advantages of massive multiple input multiple output (MIMO) in the downlink, channel state information (CSI) is required at the base station (BS) to optimize the beamforming matrices. In frequency division duplex (FDD) systems, full channel reciprocity does not hold, and CSI acquisition generally requires downlink pilot transmission followed by uplink feedback. Prior work proposed the end-to-end design of pilot transmission, feedback, and CSI estimation via deep learning. In this work, we introduce an enhanced end-to-end design that leverages partial uplink-downlink reciprocity and temporal correlation of the fading processes by utilizing jointly downlink and uplink pilots. The proposed method is based on a novel deep learning architecture -- HyperRNN -- that combines hypernetworks and recurrent neural networks (RNNs) to optimize the transfer of long-term channel features from uplink to downlink. Simulation results demonstrate that the HyperRNN achieves a lower normalized mean square error (NMSE) performance, and that it reduces requirements in terms of pilot lengths.

Smooth Bandit Optimization: Generalization to Hölder Space

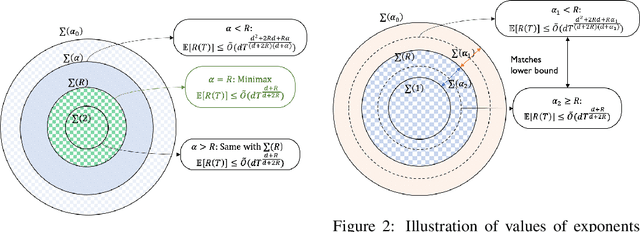
We consider bandit optimization of a smooth reward function, where the goal is cumulative regret minimization. This problem has been studied for $\alpha$-H\"older continuous (including Lipschitz) functions with $0<\alpha\leq 1$. Our main result is in generalization of the reward function to H\"older space with exponent $\alpha>1$ to bridge the gap between Lipschitz bandits and infinitely-differentiable models such as linear bandits. For H\"older continuous functions, approaches based on random sampling in bins of a discretized domain suffices as optimal. In contrast, we propose a class of two-layer algorithms that deploy misspecified linear/polynomial bandit algorithms in bins. We demonstrate that the proposed algorithm can exploit higher-order smoothness of the function by deriving a regret upper bound of $\tilde{O}(T^\frac{d+\alpha}{d+2\alpha})$ for when $\alpha>1$, which matches existing lower bound. We also study adaptation to unknown function smoothness over a continuous scale of H\"older spaces indexed by $\alpha$, with a bandit model selection approach applied with our proposed two-layer algorithms. We show that it achieves regret rate that matches the existing lower bound for adaptation within the $\alpha\leq 1$ subset.