Mean Shift Mask Transformer for Unseen Object Instance Segmentation

Segmenting unseen objects is a critical task in many different domains. For example, a robot may need to grasp an unseen object, which means it needs to visually separate this object from the background and/or other objects. Mean shift clustering is a common method in object segmentation tasks. However, the traditional mean shift clustering algorithm is not easily integrated into an end-to-end neural network training pipeline. In this work, we propose the Mean Shift Mask Transformer (MSMFormer), a new transformer architecture that simulates the von Mises-Fisher (vMF) mean shift clustering algorithm, allowing for the joint training and inference of both the feature extractor and the clustering. Its central component is a hypersphere attention mechanism, which updates object queries on a hypersphere. To illustrate the effectiveness of our method, we apply MSMFormer to Unseen Object Instance Segmentation, which yields a new state-of-the-art of 87.3 Boundary F-meansure on the real-world Object Clutter Indoor Dataset (OCID). Code is available at https://github.com/YoungSean/UnseenObjectsWithMeanShift

Relational Neural Markov Random Fields

Statistical Relational Learning (SRL) models have attracted significant attention due to their ability to model complex data while handling uncertainty. However, most of these models have been limited to discrete domains due to their limited potential functions. We introduce Relational Neural Markov Random Fields (RN-MRFs) which allow for handling of complex relational hybrid domains. The key advantage of our model is that it makes minimal data distributional assumptions and can seamlessly allow for human knowledge through potentials or relational rules. We propose a maximum pseudolikelihood estimation-based learning algorithm with importance sampling for training the neural potential parameters. Our empirical evaluations across diverse domains such as image processing and relational object mapping, clearly demonstrate its effectiveness against non-neural counterparts.

Lifted Hybrid Variational Inference

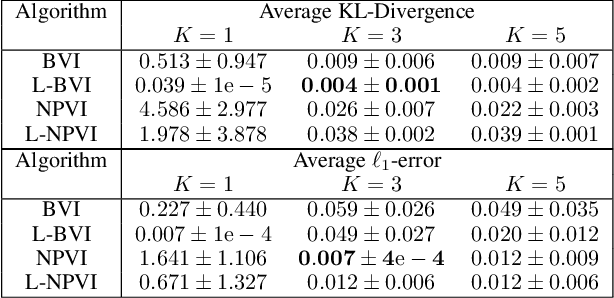
A variety of lifted inference algorithms, which exploit model symmetry to reduce computational cost, have been proposed to render inference tractable in probabilistic relational models. Most existing lifted inference algorithms operate only over discrete domains or continuous domains with restricted potential functions, e.g., Gaussian. We investigate two approximate lifted variational approaches that are applicable to hybrid domains and expressive enough to capture multi-modality. We demonstrate that the proposed variational methods are both scalable and can take advantage of approximate model symmetries, even in the presence of a large amount of continuous evidence. We demonstrate that our approach compares favorably against existing message-passing based approaches in a variety of settings. Finally, we present a sufficient condition for the Bethe approximation to yield a non-trivial estimate over the marginal polytope.