Lifted Hybrid Variational Inference
Paper and Code
Feb 08, 2020
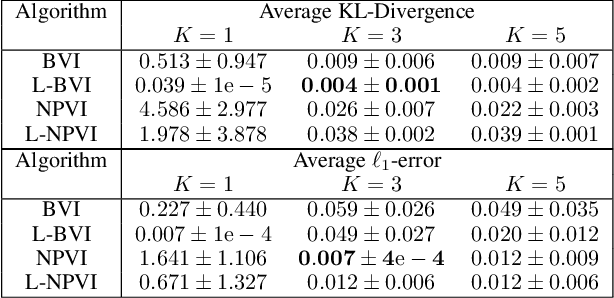


A variety of lifted inference algorithms, which exploit model symmetry to reduce computational cost, have been proposed to render inference tractable in probabilistic relational models. Most existing lifted inference algorithms operate only over discrete domains or continuous domains with restricted potential functions, e.g., Gaussian. We investigate two approximate lifted variational approaches that are applicable to hybrid domains and expressive enough to capture multi-modality. We demonstrate that the proposed variational methods are both scalable and can take advantage of approximate model symmetries, even in the presence of a large amount of continuous evidence. We demonstrate that our approach compares favorably against existing message-passing based approaches in a variety of settings. Finally, we present a sufficient condition for the Bethe approximation to yield a non-trivial estimate over the marginal polytope.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge