Model Partition and Resource Allocation for Split Learning in Vehicular Edge Networks

The integration of autonomous driving technologies with vehicular networks presents significant challenges in privacy preservation, communication efficiency, and resource allocation. This paper proposes a novel U-shaped split federated learning (U-SFL) framework to address these challenges on the way of realizing in vehicular edge networks. U-SFL is able to enhance privacy protection by keeping both raw data and labels on the vehicular user (VU) side while enabling parallel processing across multiple vehicles. To optimize communication efficiency, we introduce a semantic-aware auto-encoder (SAE) that significantly reduces the dimensionality of transmitted data while preserving essential semantic information. Furthermore, we develop a deep reinforcement learning (DRL) based algorithm to solve the NP-hard problem of dynamic resource allocation and split point selection. Our comprehensive evaluation demonstrates that U-SFL achieves comparable classification performance to traditional split learning (SL) while substantially reducing data transmission volume and communication latency. The proposed DRL-based optimization algorithm shows good convergence in balancing latency, energy consumption, and learning performance.

Reconfigurable Intelligent Surface-Aided Spectrum Sharing Coexisting with Multiple Primary Networks

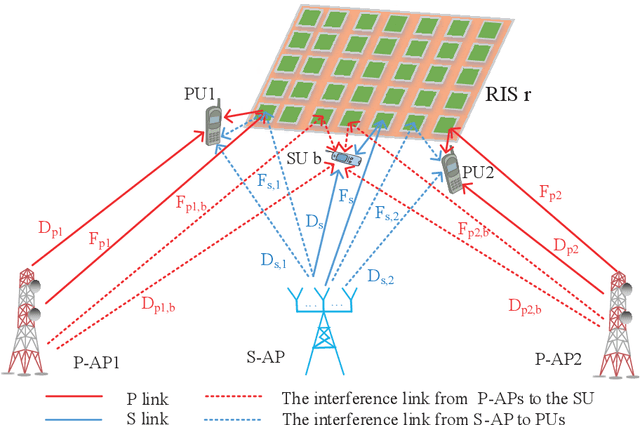
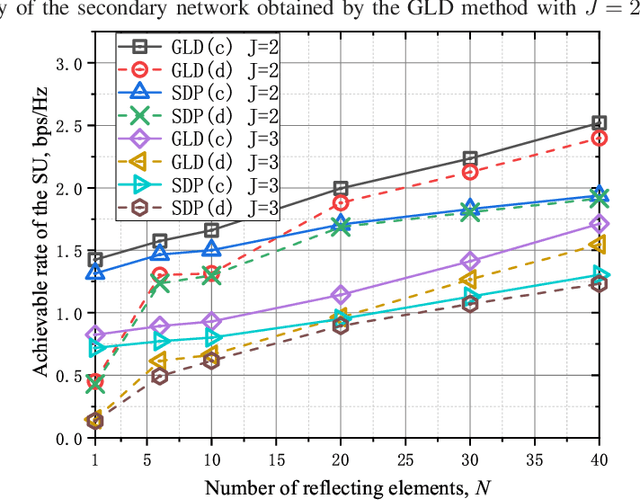
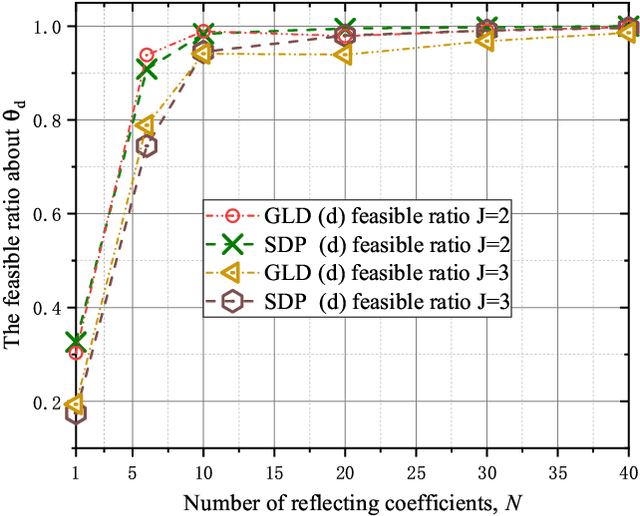
In the spectrum sharing system (SSS) coexisting with multiple primary networks, a well-designed reconfigurable intelligent surface (RIS) is employed to control the radio environments of wireless channels and relieve the scarcity of the spectrum resource in this work, which can realize high spectral efficiency (SE) and energy efficiency (EE). Specifically, the SE enhancement in the considered SSS is decomposed into two subproblems which are a second-order programming (SOP) and a fractional programming of the convex quadratic form (CQFP), respectively, to optimize alternatively the beamforming vector at the secondary access point and the reflecting coefficients at the RIS. The CQFP subproblem about optimizing the reflecting coefficients can be solved by the domain and envelope shrinking algorithm (DES), providing the best SE performance. Besides, a low-complexity method of gradient-based linearization with domain (GLD) is proposed for obtaining a sub-optimal reflecting coefficients for fast deployment. Considering the power consumption in the practical application of RIS-aided SSS, the EE performance of our proposed GLD method has significant gain over that of the SSS without RIS. The simulation results indicate the effectiveness of the DES algorithm and show that the GLD method improves the SE and EE performance in RIS-aided SSS with multiple primary networks.

Optimal Distribution Design for Irregular Repetition Slotted ALOHA with Multi-Packet Reception

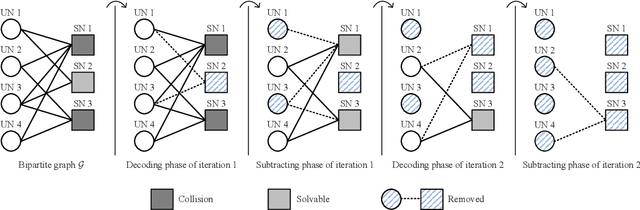
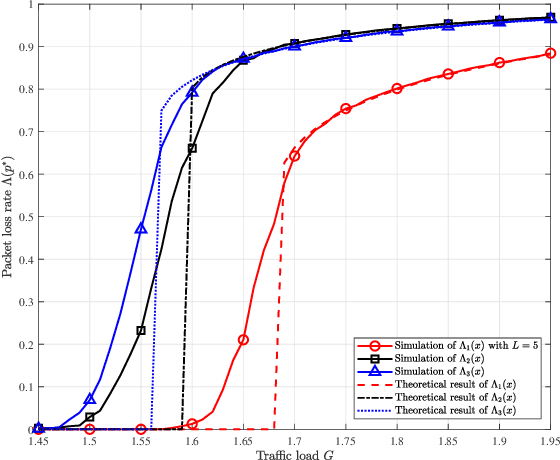
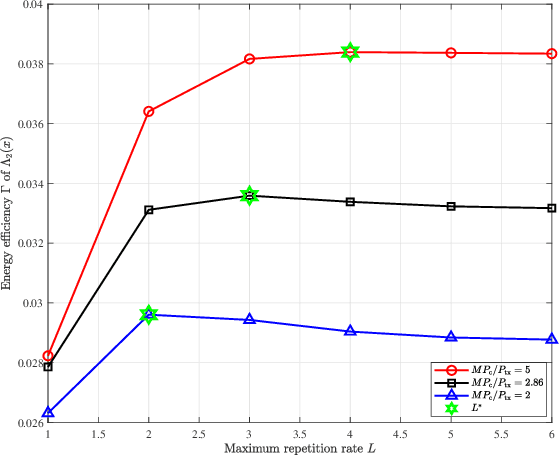
Associated with multi-packet reception at the access point, irregular repetition slotted ALOHA (IRSA) holds a great potential in improving the access capacity of massive machine type communication systems. Considering the time-frequency resource efficiency, K = 2 (multi-packet reception capability) may be the most suitable scheme for scenarios that allow smaller resource efficiency in exchange for greater throughput. In this paper, we analytically derive an optimal transmission probability distribution for IRSA with K = 2, which achieves a significant higher load threshold than the existing benchmark distributions. In addition, the energy efficiency optimization in terms of the maximum repetition rate is also presented.