Hyper-parameter optimization based on soft actor critic and hierarchical mixture regularization

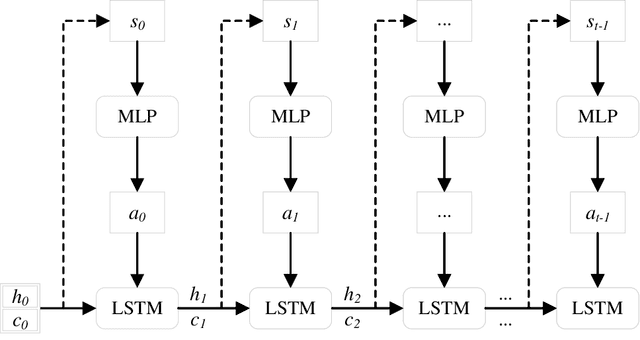
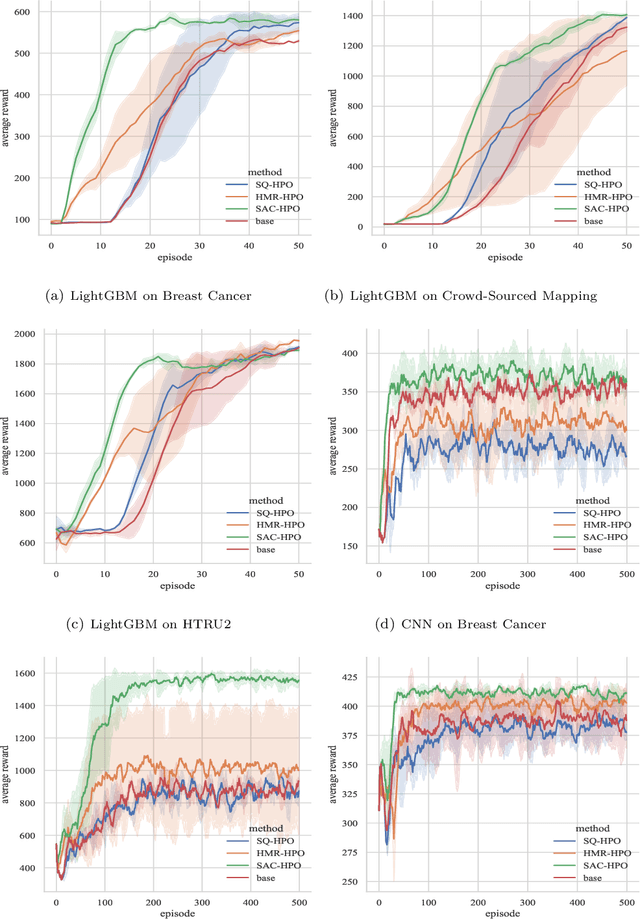
Hyper-parameter optimization is a crucial problem in machine learning as it aims to achieve the state-of-the-art performance in any model. Great efforts have been made in this field, such as random search, grid search, Bayesian optimization. In this paper, we model hyper-parameter optimization process as a Markov decision process, and tackle it with reinforcement learning. A novel hyper-parameter optimization method based on soft actor critic and hierarchical mixture regularization has been proposed. Experiments show that the proposed method can obtain better hyper-parameters in a shorter time.

Hyper-parameter estimation method with particle swarm optimization

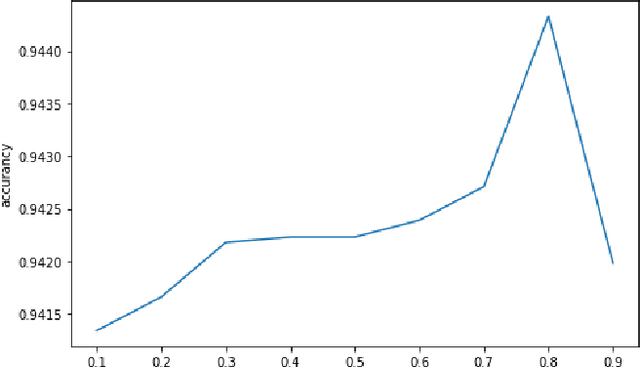
Particle swarm optimization (PSO) method cannot be directly used in the problem of hyper-parameter estimation since the mathematical formulation of the mapping from hyper-parameters to loss function or generalization accuracy is unclear. Bayesian optimization (BO) framework is capable of converting the optimization of the hyper-parameters into the optimization of an acquisition function. The acquisition function is non-convex and multi-peak. So the problem can be better solved by the PSO. The proposed method in this paper uses the particle swarm method to optimize the acquisition function in the BO framework to get better hyper-parameters. The performances of proposed method in both of the classification and regression models are evaluated and demonstrated. The results on several benchmark problems are improved.

Parallel ensemble methods for causal direction inference

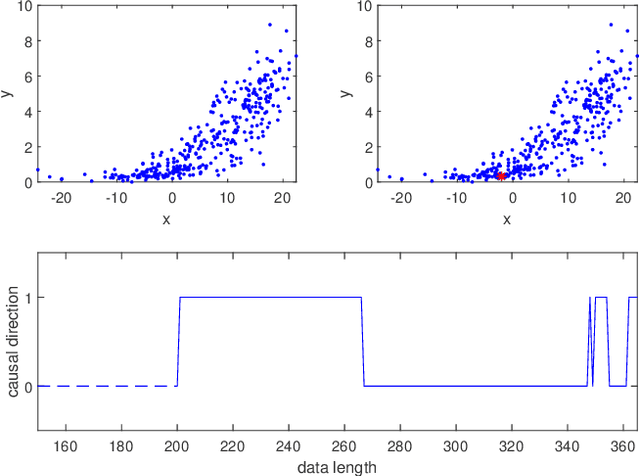
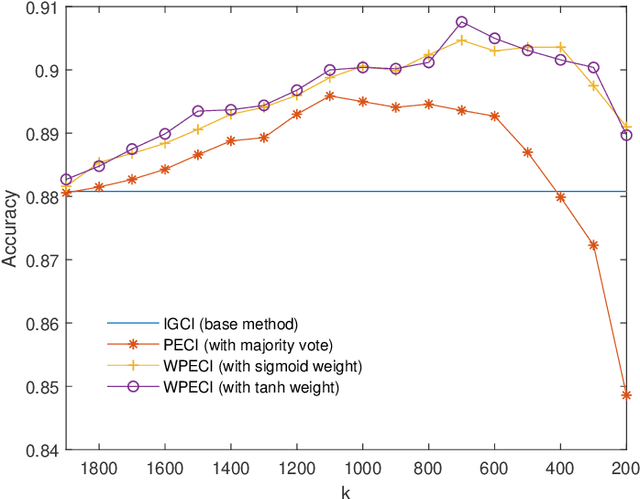
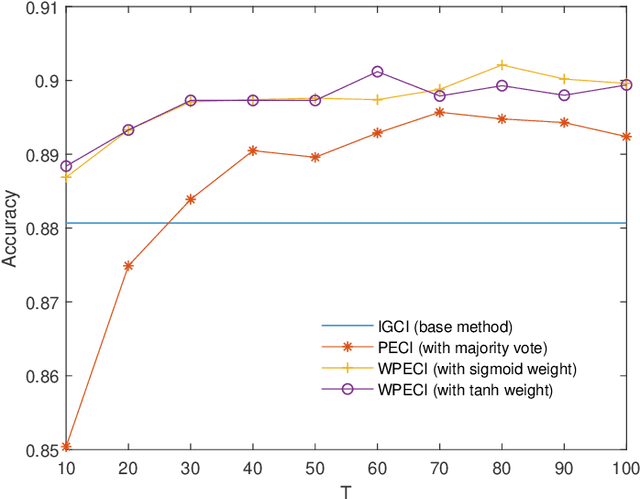
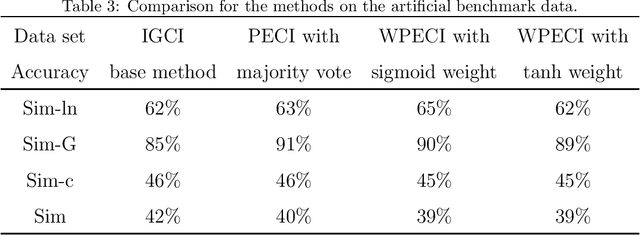
Inferring the causal direction between two variables from their observation data is one of the most fundamental and challenging topics in data science. A causal direction inference algorithm maps the observation data into a binary value which represents either x causes y or y causes x. The nature of these algorithms makes the results unstable with the change of data points. Therefore the accuracy of the causal direction inference can be improved significantly by using parallel ensemble frameworks. In this paper, new causal direction inference algorithms based on several ways of parallel ensemble are proposed. Theoretical analyses on accuracy rates are given. Experiments are done on both of the artificial data sets and the real world data sets. The accuracy performances of the methods and their computational efficiencies in parallel computing environment are demonstrated.

Attacker and Defender Counting Approach for Abstract Argumentation

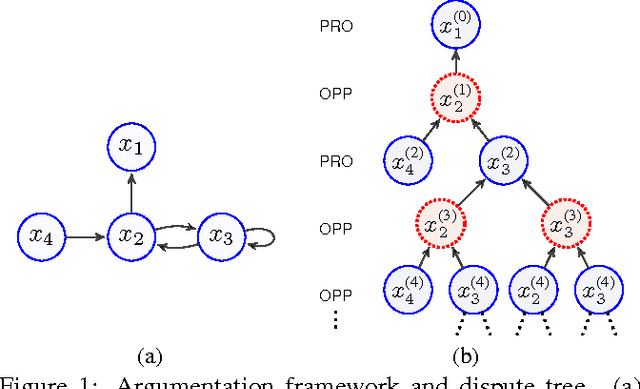
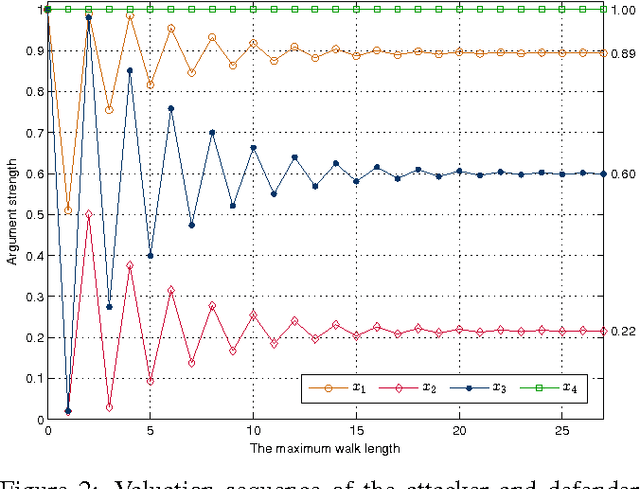
In Dung's abstract argumentation, arguments are either acceptable or unacceptable, given a chosen notion of acceptability. This gives a coarse way to compare arguments. In this paper, we propose a counting approach for a more fine-gained assessment to arguments by counting the number of their respective attackers and defenders based on argument graph and argument game. An argument is more acceptable if the proponent puts forward more number of defenders for it and the opponent puts forward less number of attackers against it. We show that our counting model has two well-behaved properties: normalization and convergence. Then, we define a counting semantics based on this model, and investigate some general properties of the semantics.

Argument Ranking with Categoriser Function

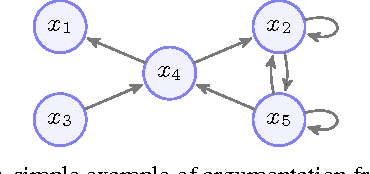
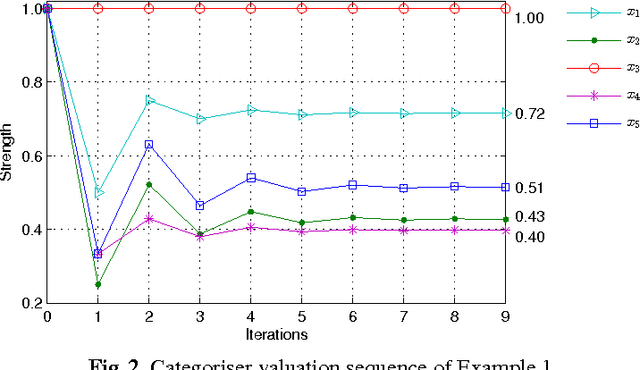
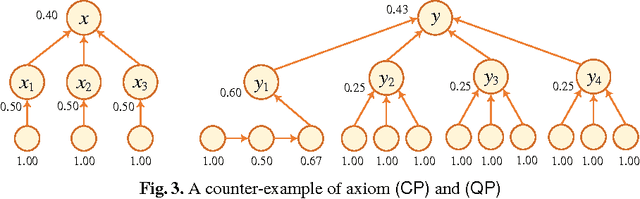
Recently, ranking-based semantics is proposed to rank-order arguments from the most acceptable to the weakest one(s), which provides a graded assessment to arguments. In general, the ranking on arguments is derived from the strength values of the arguments. Categoriser function is a common approach that assigns a strength value to a tree of arguments. When it encounters an argument system with cycles, then the categoriser strength is the solution of the non-linear equations. However, there is no detail about the existence and uniqueness of the solution, and how to find the solution (if exists). In this paper, we will cope with these issues via fixed point technique. In addition, we define the categoriser-based ranking semantics in light of categoriser strength, and investigate some general properties of it. Finally, the semantics is shown to satisfy some of the axioms that a ranking-based semantics should satisfy.