Some Supplementaries to The Counting Semantics for Abstract Argumentation

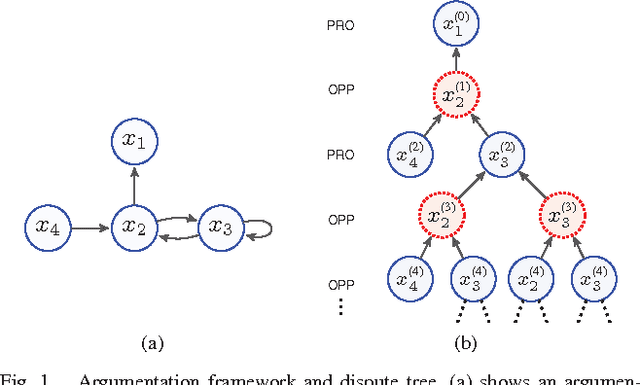
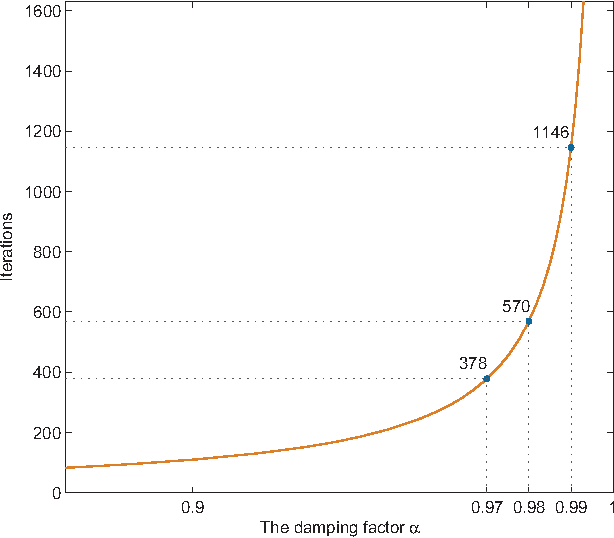
Dung's abstract argumentation framework consists of a set of interacting arguments and a series of semantics for evaluating them. Those semantics partition the powerset of the set of arguments into two classes: extensions and non-extensions. In order to reason with a specific semantics, one needs to take a credulous or skeptical approach, i.e. an argument is eventually accepted, if it is accepted in one or all extensions, respectively. In our previous work \cite{ref-pu2015counting}, we have proposed a novel semantics, called \emph{counting semantics}, which allows for a more fine-grained assessment to arguments by counting the number of their respective attackers and defenders based on argument graph and argument game. In this paper, we continue our previous work by presenting some supplementaries about how to choose the damaging factor for the counting semantics, and what relationships with some existing approaches, such as Dung's classical semantics, generic gradual valuations. Lastly, an axiomatic perspective on the ranking semantics induced by our counting semantics are presented.

Attacker and Defender Counting Approach for Abstract Argumentation

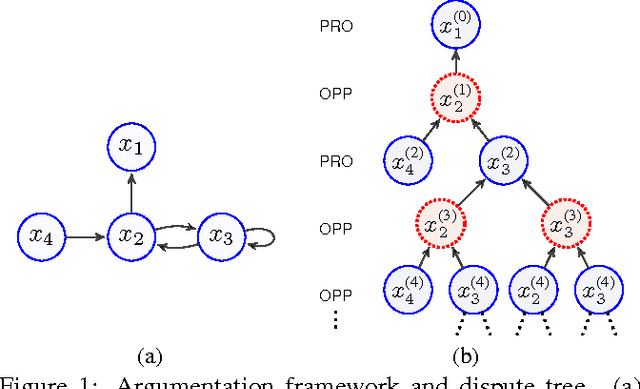
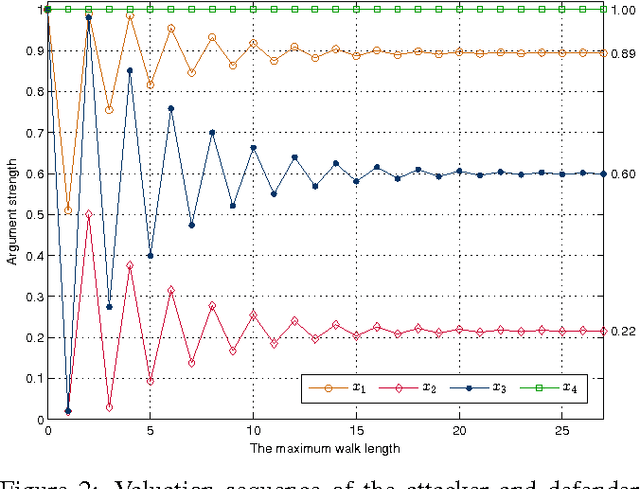
In Dung's abstract argumentation, arguments are either acceptable or unacceptable, given a chosen notion of acceptability. This gives a coarse way to compare arguments. In this paper, we propose a counting approach for a more fine-gained assessment to arguments by counting the number of their respective attackers and defenders based on argument graph and argument game. An argument is more acceptable if the proponent puts forward more number of defenders for it and the opponent puts forward less number of attackers against it. We show that our counting model has two well-behaved properties: normalization and convergence. Then, we define a counting semantics based on this model, and investigate some general properties of the semantics.

Argument Ranking with Categoriser Function

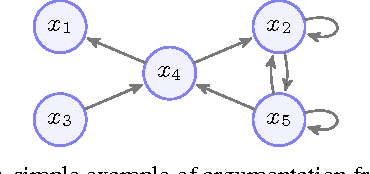
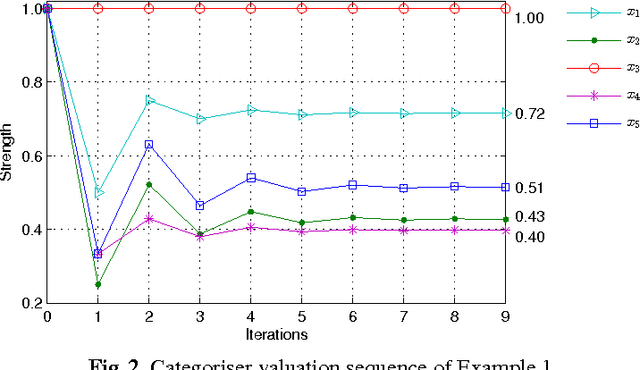
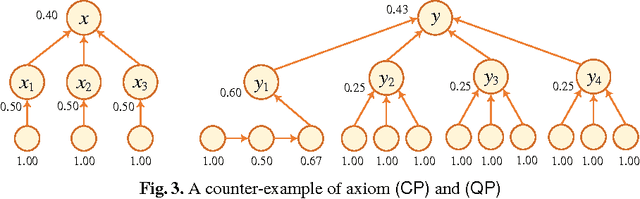
Recently, ranking-based semantics is proposed to rank-order arguments from the most acceptable to the weakest one(s), which provides a graded assessment to arguments. In general, the ranking on arguments is derived from the strength values of the arguments. Categoriser function is a common approach that assigns a strength value to a tree of arguments. When it encounters an argument system with cycles, then the categoriser strength is the solution of the non-linear equations. However, there is no detail about the existence and uniqueness of the solution, and how to find the solution (if exists). In this paper, we will cope with these issues via fixed point technique. In addition, we define the categoriser-based ranking semantics in light of categoriser strength, and investigate some general properties of it. Finally, the semantics is shown to satisfy some of the axioms that a ranking-based semantics should satisfy.