Argument Ranking with Categoriser Function
Paper and Code
Jul 16, 2014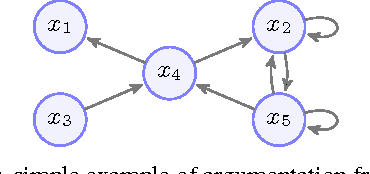
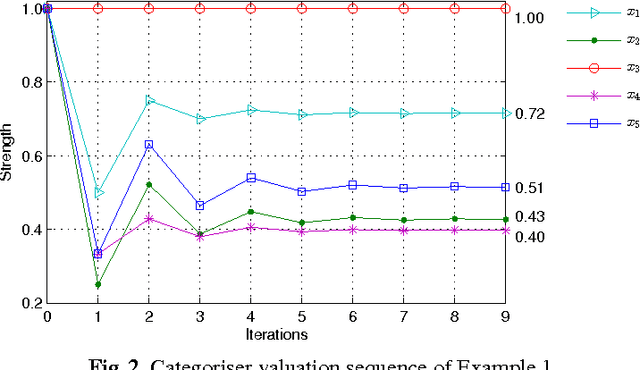
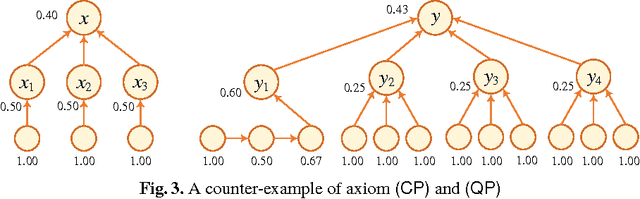
Recently, ranking-based semantics is proposed to rank-order arguments from the most acceptable to the weakest one(s), which provides a graded assessment to arguments. In general, the ranking on arguments is derived from the strength values of the arguments. Categoriser function is a common approach that assigns a strength value to a tree of arguments. When it encounters an argument system with cycles, then the categoriser strength is the solution of the non-linear equations. However, there is no detail about the existence and uniqueness of the solution, and how to find the solution (if exists). In this paper, we will cope with these issues via fixed point technique. In addition, we define the categoriser-based ranking semantics in light of categoriser strength, and investigate some general properties of it. Finally, the semantics is shown to satisfy some of the axioms that a ranking-based semantics should satisfy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge