Predicting Dynamics of Ultra-Large Complex Systems by Inferring Governing Equations

Predicting the behavior of ultra-large complex systems, from climate to biological and technological networks, is a central unsolved challenge. Existing approaches face a fundamental trade-off: equation discovery methods provide interpretability but fail to scale, while neural networks scale but operate as black boxes and often lose reliability over long times. Here, we introduce the Sparse Identification Graph Neural Network, a framework that overcome this divide by allowing to infer the governing equations of large networked systems from data. By defining symbolic discovery as edge-level information, SIGN decouples the scalability of sparse identification from network size, enabling efficient equation discovery even in large systems. SIGN allows to study networks with over 100,000 nodes while remaining robust to noise, sparse sampling, and missing data. Across diverse benchmark systems, including coupled chaotic oscillators, neural dynamics, and epidemic spreading, it recovers governing equations with high precision and sustains accurate long-term predictions. Applied to a data set of time series of temperature measurements in 71,987 sea surface positions, SIGN identifies a compact predictive network model and captures large-scale sea surface temperature conditions up to two years in advance. By enabling equation discovery at previously inaccessible scales, SIGN opens a path toward interpretable and reliable prediction of real-world complex systems.

Improving the Stability of GNN Force Field Models by Reducing Feature Correlation

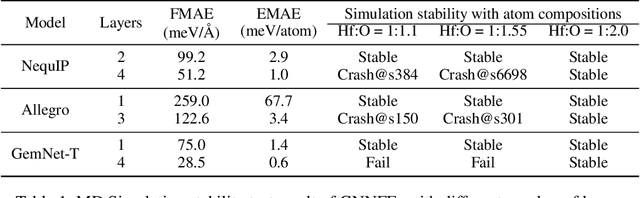
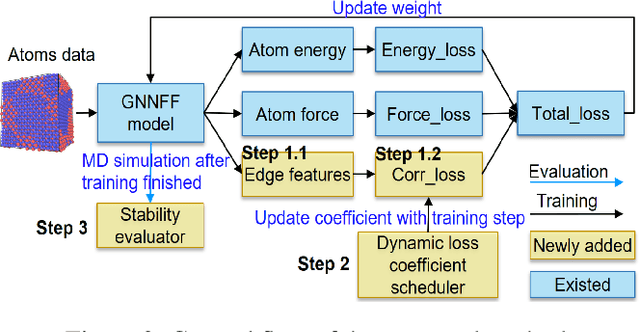
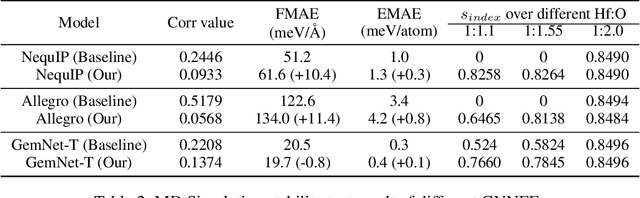
Recently, Graph Neural Network based Force Field (GNNFF) models are widely used in Molecular Dynamics (MD) simulation, which is one of the most cost-effective means in semiconductor material research. However, even such models provide high accuracy in energy and force Mean Absolute Error (MAE) over trained (in-distribution) datasets, they often become unstable during long-time MD simulation when used for out-of-distribution datasets. In this paper, we propose a feature correlation based method for GNNFF models to enhance the stability of MD simulation. We reveal the negative relationship between feature correlation and the stability of GNNFF models, and design a loss function with a dynamic loss coefficient scheduler to reduce edge feature correlation that can be applied in general GNNFF training. We also propose an empirical metric to evaluate the stability in MD simulation. Experiments show our method can significantly improve stability for GNNFF models especially in out-of-distribution data with less than 3% computational overhead. For example, we can ensure the stable MD simulation time from 0.03ps to 10ps for Allegro model.

Cooperative Network Learning for Large-Scale and Decentralized Graphs

Graph research, the systematic study of interconnected data points represented as graphs, plays a vital role in capturing intricate relationships within networked systems. However, in the real world, as graphs scale up, concerns about data security among different data-owning agencies arise, hindering information sharing and, ultimately, the utilization of graph data. Therefore, establishing a mutual trust mechanism among graph agencies is crucial for unlocking the full potential of graphs. Here, we introduce a Cooperative Network Learning (CNL) framework to ensure secure graph computing for various graph tasks. Essentially, this CNL framework unifies the local and global perspectives of GNN computing with distributed data for an agency by virtually connecting all participating agencies as a global graph without a fixed central coordinator. Inter-agency computing is protected by various technologies inherent in our framework, including homomorphic encryption and secure transmission. Moreover, each agency has a fair right to design or employ various graph learning models from its local or global perspective. Thus, CNL can collaboratively train GNN models based on decentralized graphs inferred from local and global graphs. Experiments on contagion dynamics prediction and traditional graph tasks (i.e., node classification and link prediction) demonstrate that our CNL architecture outperforms state-of-the-art GNNs developed at individual sites, revealing that CNL can provide a reliable, fair, secure, privacy-preserving, and global perspective to build effective and personalized models for network applications. We hope this framework will address privacy concerns in graph-related research and integrate decentralized graph data structures to benefit the network research community in cooperation and innovation.

Higher-order Graph Convolutional Network with Flower-Petals Laplacians on Simplicial Complexes

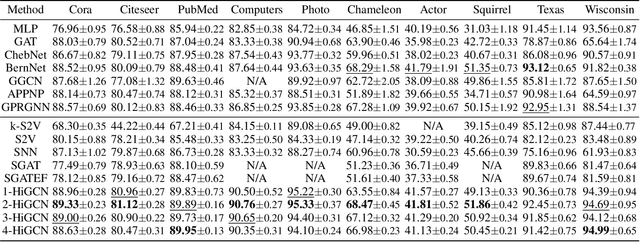
Despite the recent successes of vanilla Graph Neural Networks (GNNs) on many tasks, their foundation on pairwise interaction networks inherently limits their capacity to discern latent higher-order interactions in complex systems. To bridge this capability gap, we propose a novel approach exploiting the rich mathematical theory of simplicial complexes (SCs) - a robust tool for modeling higher-order interactions. Current SC-based GNNs are burdened by high complexity and rigidity, and quantifying higher-order interaction strengths remains challenging. Innovatively, we present a higher-order Flower-Petals (FP) model, incorporating FP Laplacians into SCs. Further, we introduce a Higher-order Graph Convolutional Network (HiGCN) grounded in FP Laplacians, capable of discerning intrinsic features across varying topological scales. By employing learnable graph filters, a parameter group within each FP Laplacian domain, we can identify diverse patterns where the filters' weights serve as a quantifiable measure of higher-order interaction strengths. The theoretical underpinnings of HiGCN's advanced expressiveness are rigorously demonstrated. Additionally, our empirical investigations reveal that the proposed model accomplishes state-of-the-art (SOTA) performance on a range of graph tasks and provides a scalable and flexible solution to explore higher-order interactions in graphs.

Influential Simplices Mining via Simplicial Convolutional Network

Simplicial complexes have recently been in the limelight of higher-order network analysis, where a minority of simplices play crucial roles in structures and functions due to network heterogeneity. We find a significant inconsistency between identifying influential nodes and simplices. Therefore, it remains elusive how to characterize simplices' influence and identify influential simplices, despite the relative maturity of research on influential nodes (0-simplices) identification. Meanwhile, graph neural networks (GNNs) are potent tools that can exploit network topology and node features simultaneously, but they struggle to tackle higher-order tasks. In this paper, we propose a higher-order graph learning model, named influential simplices mining neural network (ISMnet), to identify vital h-simplices in simplicial complexes. It can tackle higher-order tasks by leveraging novel higher-order presentations: hierarchical bipartite graphs and higher-order hierarchical (HoH) Laplacians, where targeted simplices are grouped into a hub set and can interact with other simplices. Furthermore, ISMnet employs learnable graph convolutional operators in each HoH Laplacian domain to capture interactions among simplices, and it can identify influential simplices of arbitrary order by changing the hub set. Empirical results demonstrate that ISMnet significantly outperforms existing methods in ranking 0-simplices (nodes) and 2-simplices. In general, this novel framework excels in identifying influential simplices and promises to serve as a potent tool in higher-order network analysis.