Differentiable Bilevel Programming for Stackelberg Congestion Games

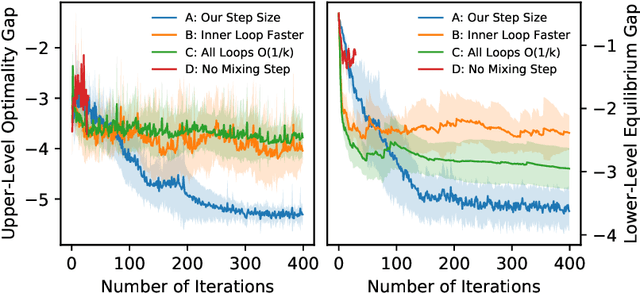
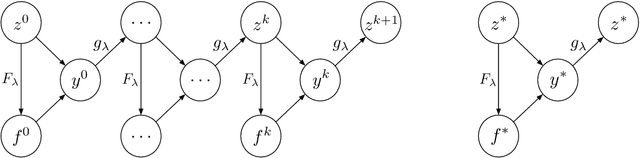
A Stackelberg congestion game (SCG) is a bilevel program in which a leader aims to maximize their own gain by anticipating and manipulating the equilibrium state at which followers settle by playing a congestion game. Large-scale SCGs are well known for their intractability and complexity. This study approaches SCGs through differentiable programming, which marries the latest developments in machine learning with conventional methodologies. The core idea centers on representing the lower-level equilibrium problem using an evolution path formed by the imitative logit dynamics. It enables the use of automatic differentiation over the evolution path towards equilibrium, leading to a double-loop gradient descent algorithm. We further show the fixation on the lower-level equilibrium may be a self-imposed computational obstacle. Instead, the leader may only look ahead along the followers' evolution path for a few steps, while updating their decisions in sync with the followers through a co-evolution process. The revelation gives rise to a single-loop algorithm that is more efficient in terms of both memory consumption and computation time. Through numerical experiments that cover a wide range of benchmark problems, we find the single-loop algorithm consistently strikes a good balance between solution quality and efficiency, outperforming not only the standard double-loop implementation but also other methods from the literature. Importantly, our results highlight both the wastefulness of "full anticipation" and the peril of "zero anticipation". If a quick-and-dirty heuristic is needed for solving a really large SCG, the proposed single-loop algorithm with a one-step look-ahead makes an ideal candidate.

Inducing Equilibria via Incentives: Simultaneous Design-and-Play Finds Global Optima

To regulate a social system comprised of self-interested agents, economic incentives (e.g., taxes, tolls, and subsidies) are often required to induce a desirable outcome. This incentive design problem naturally possesses a bi-level structure, in which an upper-level "designer" modifies the payoffs of the agents with incentives while anticipating the response of the agents at the lower level, who play a non-cooperative game that converges to an equilibrium. The existing bi-level optimization algorithms developed in machine learning raise a dilemma when applied to this problem: anticipating how incentives affect the agents at equilibrium requires solving the equilibrium problem repeatedly, which is computationally inefficient; bypassing the time-consuming step of equilibrium-finding can reduce the computational cost, but may lead the designer to a sub-optimal solution. To address such a dilemma, we propose a method that tackles the designer's and agents' problems simultaneously in a single loop. In particular, at each iteration, both the designer and the agents only move one step based on the first-order information. In the proposed scheme, although the designer does not solve the equilibrium problem repeatedly, it can anticipate the overall influence of the incentives on the agents, which guarantees optimality. We prove that the algorithm converges to the global optima at a sublinear rate for a broad class of games.

End-to-End Learning and Intervention in Games

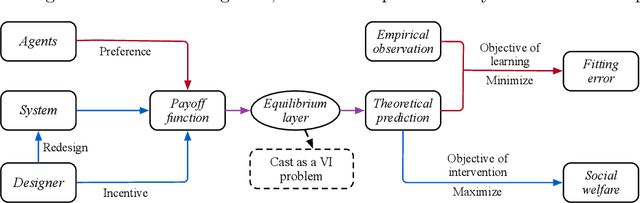
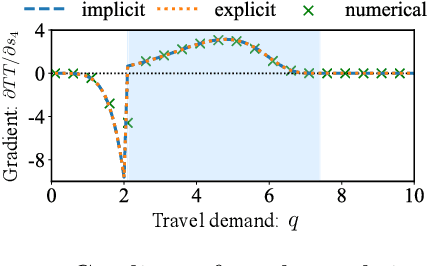
In a social system, the self-interest of agents can be detrimental to the collective good, sometimes leading to social dilemmas. To resolve such a conflict, a central designer may intervene by either redesigning the system or incentivizing the agents to change their behaviors. To be effective, the designer must anticipate how the agents react to the intervention, which is dictated by their often unknown payoff functions. Therefore, learning about the agents is a prerequisite for intervention. In this paper, we provide a unified framework for learning and intervention in games. We cast the equilibria of games as individual layers and integrate them into an end-to-end optimization framework. To enable the backward propagation through the equilibria of games, we propose two approaches, respectively based on explicit and implicit differentiation. Specifically, we cast the equilibria as the solutions to variational inequalities (VIs). The explicit approach unrolls the projection method for solving VIs, while the implicit approach exploits the sensitivity of the solutions to VIs. At the core of both approaches is the differentiation through a projection operator. Moreover, we establish the correctness of both approaches and identify the conditions under which one approach is more desirable than the other. The analytical results are validated using several real-world problems.