Inducing Equilibria via Incentives: Simultaneous Design-and-Play Finds Global Optima
Paper and Code
Oct 12, 2021
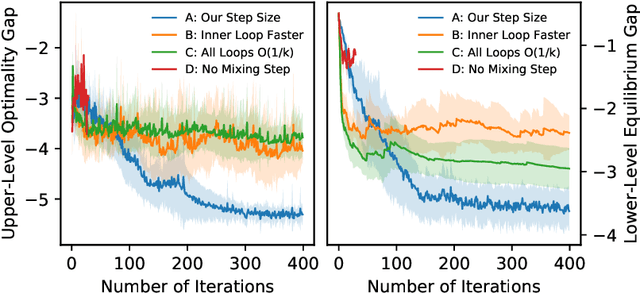
To regulate a social system comprised of self-interested agents, economic incentives (e.g., taxes, tolls, and subsidies) are often required to induce a desirable outcome. This incentive design problem naturally possesses a bi-level structure, in which an upper-level "designer" modifies the payoffs of the agents with incentives while anticipating the response of the agents at the lower level, who play a non-cooperative game that converges to an equilibrium. The existing bi-level optimization algorithms developed in machine learning raise a dilemma when applied to this problem: anticipating how incentives affect the agents at equilibrium requires solving the equilibrium problem repeatedly, which is computationally inefficient; bypassing the time-consuming step of equilibrium-finding can reduce the computational cost, but may lead the designer to a sub-optimal solution. To address such a dilemma, we propose a method that tackles the designer's and agents' problems simultaneously in a single loop. In particular, at each iteration, both the designer and the agents only move one step based on the first-order information. In the proposed scheme, although the designer does not solve the equilibrium problem repeatedly, it can anticipate the overall influence of the incentives on the agents, which guarantees optimality. We prove that the algorithm converges to the global optima at a sublinear rate for a broad class of games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge