Young Woong Park
Integrated Subset Selection and Bandwidth Estimation Algorithm for Geographically Weighted Regression
Mar 21, 2025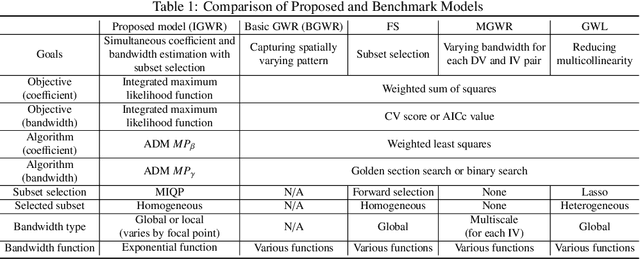
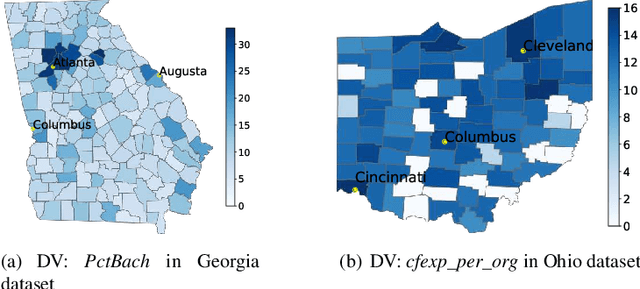
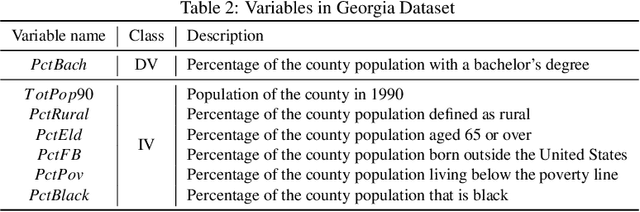
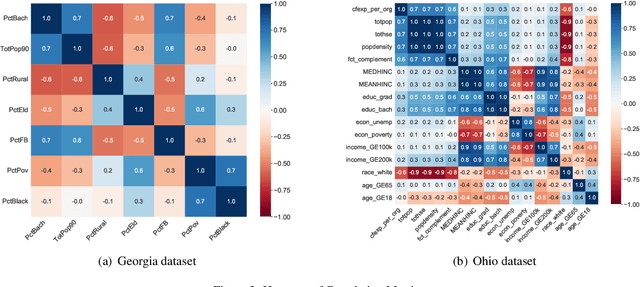
Abstract:This study proposes a mathematical programming-based algorithm for the integrated selection of variable subsets and bandwidth estimation in geographically weighted regression, a local regression method that allows the kernel bandwidth and regression coefficients to vary across study areas. Unlike standard approaches in the literature, in which bandwidth and regression parameters are estimated separately for each focal point on the basis of different criteria, our model uses a single objective function for the integrated estimation of regression and bandwidth parameters across all focal points, based on the regression likelihood function and variance modeling. The proposed model further integrates a procedure to select a single subset of independent variables for all focal points, whereas existing approaches may return heterogeneous subsets across focal points. We then propose an alternative direction method to solve the nonconvex mathematical model and show that it converges to a partial minimum. The computational experiment indicates that the proposed algorithm provides competitive explanatory power with stable spatially varying patterns, with the ability to select the best subset and account for additional constraints.
Discordance Minimization-based Imputation Algorithms for Missing Values in Rating Data
Nov 07, 2023Abstract:Ratings are frequently used to evaluate and compare subjects in various applications, from education to healthcare, because ratings provide succinct yet credible measures for comparing subjects. However, when multiple rating lists are combined or considered together, subjects often have missing ratings, because most rating lists do not rate every subject in the combined list. In this study, we propose analyses on missing value patterns using six real-world data sets in various applications, as well as the conditions for applicability of imputation algorithms. Based on the special structures and properties derived from the analyses, we propose optimization models and algorithms that minimize the total rating discordance across rating providers to impute missing ratings in the combined rating lists, using only the known rating information. The total rating discordance is defined as the sum of the pairwise discordance metric, which can be written as a quadratic function. Computational experiments based on real-world and synthetic rating data sets show that the proposed methods outperform the state-of-the-art general imputation methods in the literature in terms of imputation accuracy.
A Mathematical Programming Approach for Integrated Multiple Linear Regression Subset Selection and Validation
Dec 12, 2017
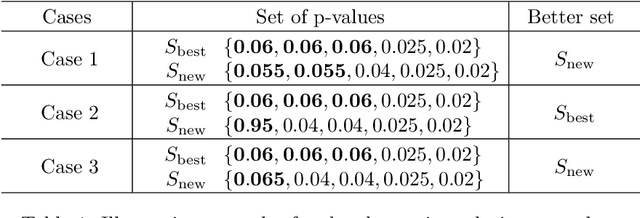
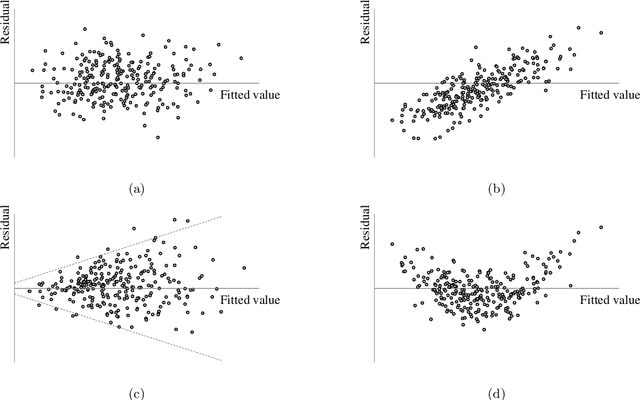
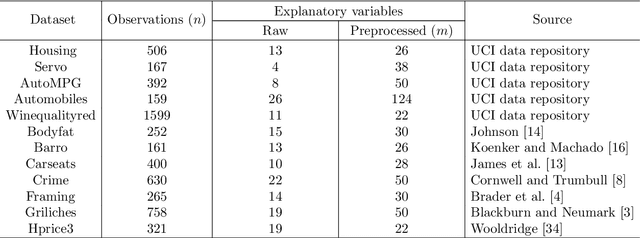
Abstract:Subset selection for multiple linear regression aims to construct a regression model that minimizes errors by selecting a small number of explanatory variables. Once a model is built, various statistical tests and diagnostics are conducted to validate the model and to determine whether regression assumptions are met. Most traditional approaches require human decisions at this step, for example, the user adding or removing a variable until a satisfactory model is obtained. However, this trial-and-error strategy cannot guarantee that a subset that minimizes the errors while satisfying all regression assumptions will be found. In this paper, we propose a fully automated model building procedure for multiple linear regression subset selection that integrates model building and validation based on mathematical programming. The proposed model minimizes mean squared errors while ensuring that the majority of the important regression assumptions are met. When no subset satisfies all of the considered regression assumptions, our model provides an alternative subset that satisfies most of these assumptions. Computational results show that our model yields better solutions (i.e., satisfying more regression assumptions) compared to benchmark models while maintaining similar explanatory power.
Optimization for L1-Norm Error Fitting via Data Aggregation
Nov 01, 2017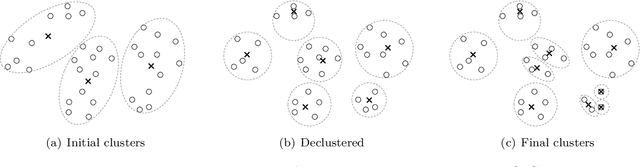
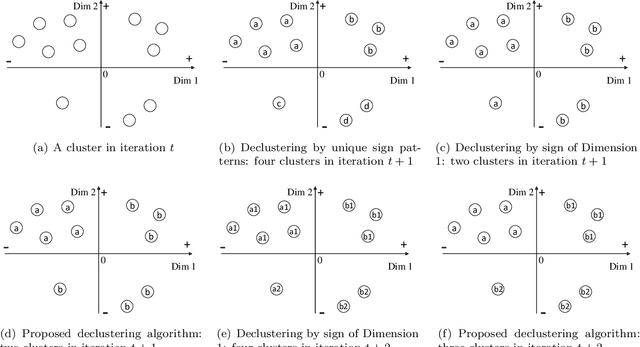
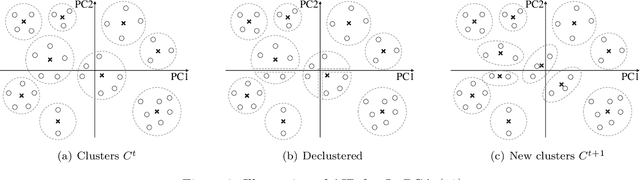
Abstract:We propose a data aggregation-based algorithm with monotonic convergence to a global optimum for a generalized version of the L1-norm error fitting model with an assumption of the fitting function. Any L1-norm model can be solved optimally using the proposed algorithm if it follows the form of the L1-norm error fitting problem and if the fitting function satisfies the assumption. The proposed algorithm can also solve multi-dimensional fitting problems with arbitrary constraints on the fitting coefficients matrix. The generalized problem includes popular models such as regression, principal component analysis, and the orthogonal Procrustes problem. The results of the computational experiment show that the proposed algorithms are up to 9,000 times faster than the state-of-the-art benchmarks for the problems and datasets studied.
Bayesian Network Learning via Topological Order
Aug 20, 2017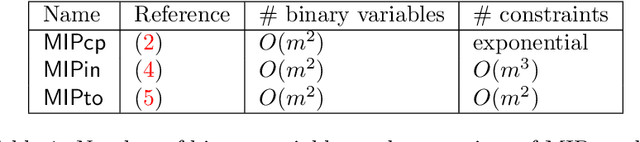
Abstract:We propose a mixed integer programming (MIP) model and iterative algorithms based on topological orders to solve optimization problems with acyclic constraints on a directed graph. The proposed MIP model has a significantly lower number of constraints compared to popular MIP models based on cycle elimination constraints and triangular inequalities. The proposed iterative algorithms use gradient descent and iterative reordering approaches, respectively, for searching topological orders. A computational experiment is presented for the Gaussian Bayesian network learning problem, an optimization problem minimizing the sum of squared errors of regression models with L1 penalty over a feature network with application of gene network inference in bioinformatics.
Subset Selection for Multiple Linear Regression via Optimization
Jan 27, 2017
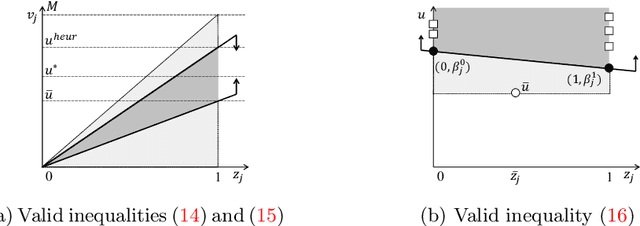

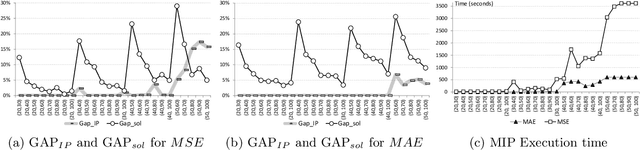
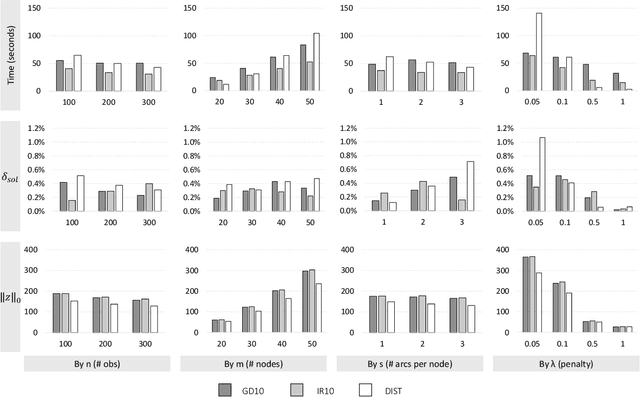
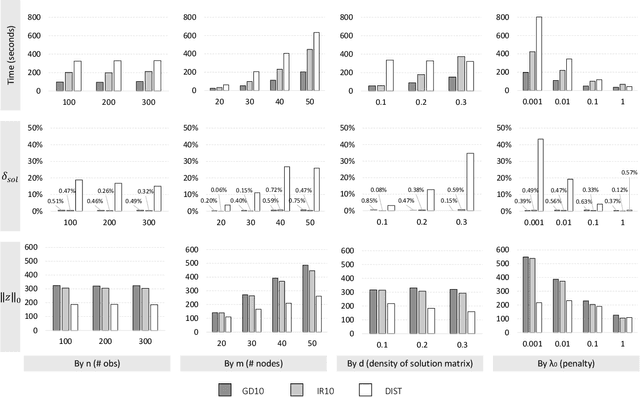
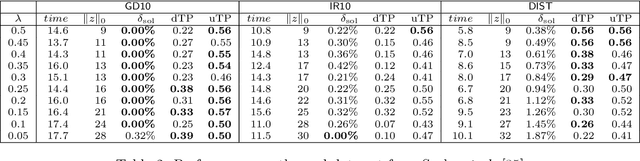
Abstract:Subset selection in multiple linear regression is to choose a subset of candidate explanatory variables that tradeoff error and the number of variables selected. We built mathematical programming models for subset selection and compare the performance of an LP-based branch-and-bound algorithm with tailored valid inequalities to known heuristics. We found that our models quickly find a quality solution while the rest of the time is spent to prove optimality. Our models are also applicable with slight modifications to the case with more candidate explanatory variables than observations. For this case, we provide mathematical programming models, propose new criteria, and develop heuristic algorithms based on mathematical programming.
Iteratively Reweighted Least Squares Algorithms for L1-Norm Principal Component Analysis
Sep 19, 2016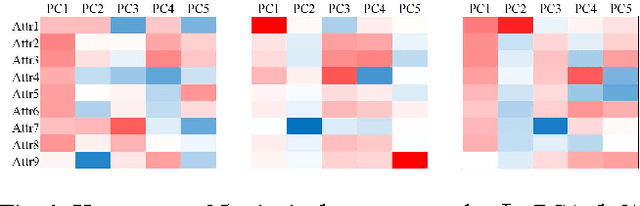



Abstract:Principal component analysis (PCA) is often used to reduce the dimension of data by selecting a few orthonormal vectors that explain most of the variance structure of the data. L1 PCA uses the L1 norm to measure error, whereas the conventional PCA uses the L2 norm. For the L1 PCA problem minimizing the fitting error of the reconstructed data, we propose an exact reweighted and an approximate algorithm based on iteratively reweighted least squares. We provide convergence analyses, and compare their performance against benchmark algorithms in the literature. The computational experiment shows that the proposed algorithms consistently perform best.
Algorithms for Generalized Cluster-wise Linear Regression
Jul 11, 2016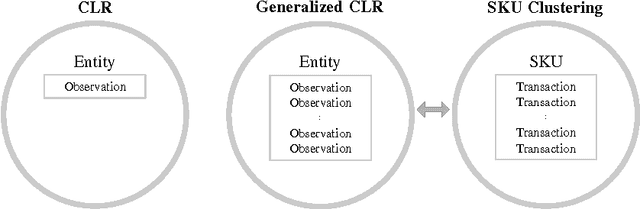

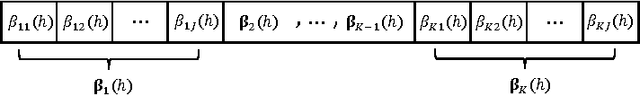
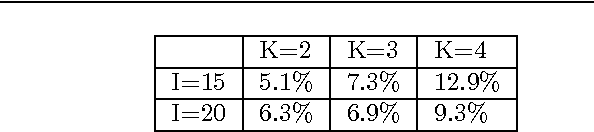
Abstract:Cluster-wise linear regression (CLR), a clustering problem intertwined with regression, is to find clusters of entities such that the overall sum of squared errors from regressions performed over these clusters is minimized, where each cluster may have different variances. We generalize the CLR problem by allowing each entity to have more than one observation, and refer to it as generalized CLR. We propose an exact mathematical programming based approach relying on column generation, a column generation based heuristic algorithm that clusters predefined groups of entities, a metaheuristic genetic algorithm with adapted Lloyd's algorithm for K-means clustering, a two-stage approach, and a modified algorithm of Sp{\"a}th \cite{Spath1979} for solving generalized CLR. We examine the performance of our algorithms on a stock keeping unit (SKU) clustering problem employed in forecasting halo and cannibalization effects in promotions using real-world retail data from a large supermarket chain. In the SKU clustering problem, the retailer needs to cluster SKUs based on their seasonal effects in response to promotions. The seasonal effects are the results of regressions with predictors being promotion mechanisms and seasonal dummies performed over clusters generated. We compare the performance of all proposed algorithms for the SKU problem with real-world and synthetic data.
An Aggregate and Iterative Disaggregate Algorithm with Proven Optimality in Machine Learning
Jul 05, 2016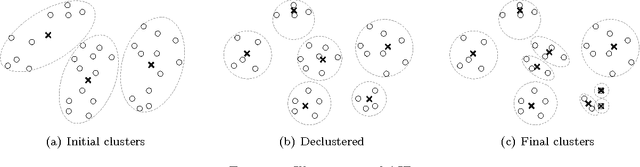
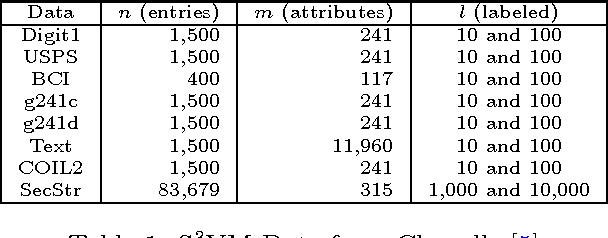
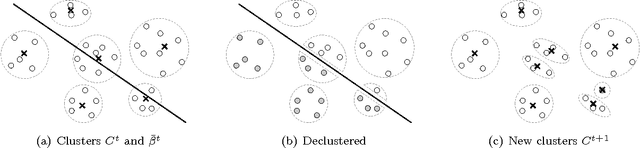
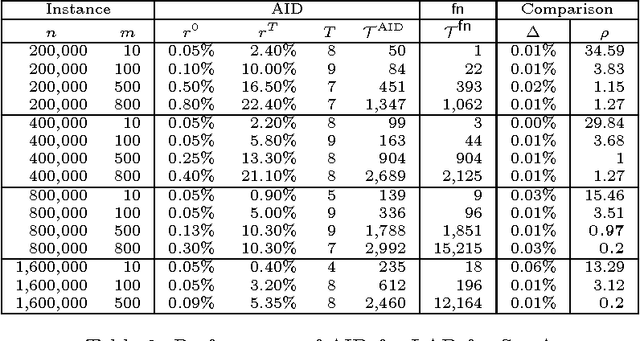
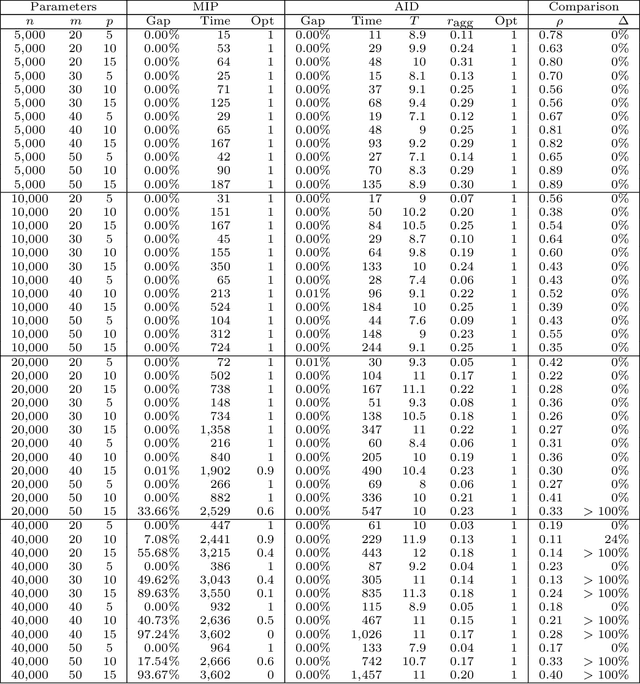
Abstract:We propose a clustering-based iterative algorithm to solve certain optimization problems in machine learning, where we start the algorithm by aggregating the original data, solving the problem on aggregated data, and then in subsequent steps gradually disaggregate the aggregated data. We apply the algorithm to common machine learning problems such as the least absolute deviation regression problem, support vector machines, and semi-supervised support vector machines. We derive model-specific data aggregation and disaggregation procedures. We also show optimality, convergence, and the optimality gap of the approximated solution in each iteration. A computational study is provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge