Optimization for L1-Norm Error Fitting via Data Aggregation

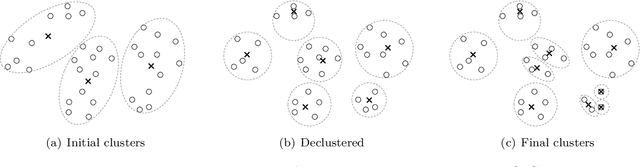
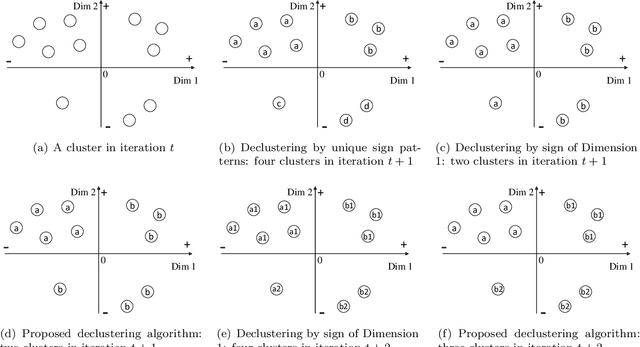
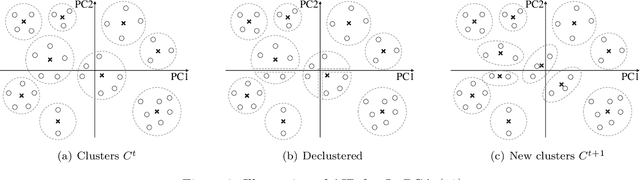
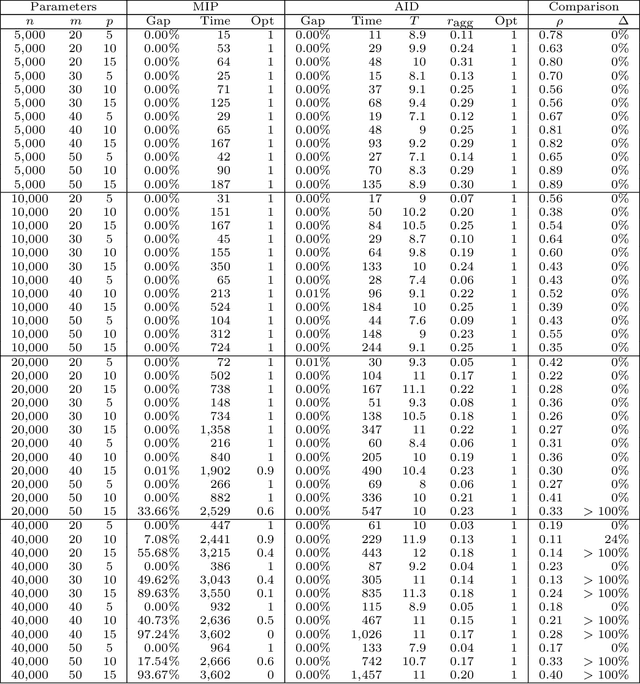
We propose a data aggregation-based algorithm with monotonic convergence to a global optimum for a generalized version of the L1-norm error fitting model with an assumption of the fitting function. Any L1-norm model can be solved optimally using the proposed algorithm if it follows the form of the L1-norm error fitting problem and if the fitting function satisfies the assumption. The proposed algorithm can also solve multi-dimensional fitting problems with arbitrary constraints on the fitting coefficients matrix. The generalized problem includes popular models such as regression, principal component analysis, and the orthogonal Procrustes problem. The results of the computational experiment show that the proposed algorithms are up to 9,000 times faster than the state-of-the-art benchmarks for the problems and datasets studied.