Decentralized Deep Learning using Momentum-Accelerated Consensus

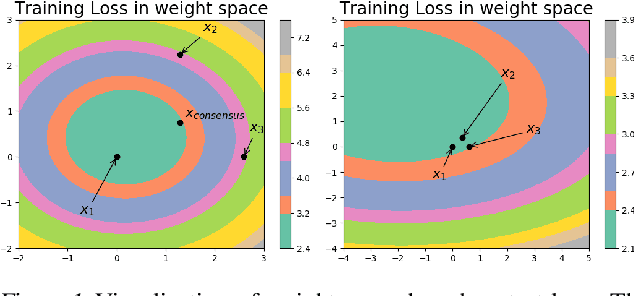
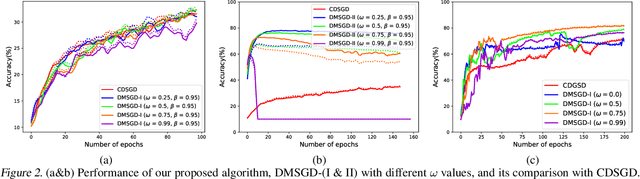
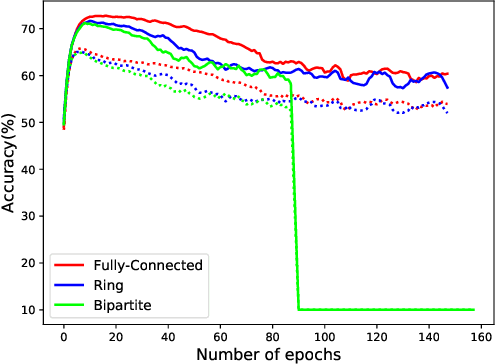
We consider the problem of decentralized deep learning where multiple agents collaborate to learn from a distributed dataset. While there exist several decentralized deep learning approaches, the majority consider a central parameter-server topology for aggregating the model parameters from the agents. However, such a topology may be inapplicable in networked systems such as ad-hoc mobile networks, field robotics, and power network systems where direct communication with the central parameter server may be inefficient. In this context, we propose and analyze a novel decentralized deep learning algorithm where the agents interact over a fixed communication topology (without a central server). Our algorithm is based on the heavy-ball acceleration method used in gradient-based optimization. We propose a novel consensus protocol where each agent shares with its neighbors its model parameters as well as gradient-momentum values during the optimization process. We consider both strongly convex and non-convex objective functions and theoretically analyze our algorithm's performance. We present several empirical comparisons with competing decentralized learning methods to demonstrate the efficacy of our approach under different communication topologies.

On Higher-order Moments in Adam

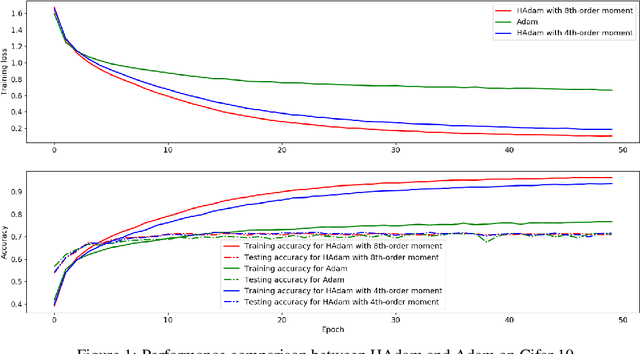
In this paper, we investigate the popular deep learning optimization routine, Adam, from the perspective of statistical moments. While Adam is an adaptive lower-order moment based (of the stochastic gradient) method, we propose an extension namely, HAdam, which uses higher order moments of the stochastic gradient. Our analysis and experiments reveal that certain higher-order moments of the stochastic gradient are able to achieve better performance compared to the vanilla Adam algorithm. We also provide some analysis of HAdam related to odd and even moments to explain some intriguing and seemingly non-intuitive empirical results.