How to Do Machine Learning with Small Data? -- A Review from an Industrial Perspective

Artificial intelligence experienced a technological breakthrough in science, industry, and everyday life in the recent few decades. The advancements can be credited to the ever-increasing availability and miniaturization of computational resources that resulted in exponential data growth. However, because of the insufficient amount of data in some cases, employing machine learning in solving complex tasks is not straightforward or even possible. As a result, machine learning with small data experiences rising importance in data science and application in several fields. The authors focus on interpreting the general term of "small data" and their engineering and industrial application role. They give a brief overview of the most important industrial applications of machine learning and small data. Small data is defined in terms of various characteristics compared to big data, and a machine learning formalism was introduced. Five critical challenges of machine learning with small data in industrial applications are presented: unlabeled data, imbalanced data, missing data, insufficient data, and rare events. Based on those definitions, an overview of the considerations in domain representation and data acquisition is given along with a taxonomy of machine learning approaches in the context of small data.

Direct Variational Perspective Shape from Shading with Cartesian Depth Parametrisation

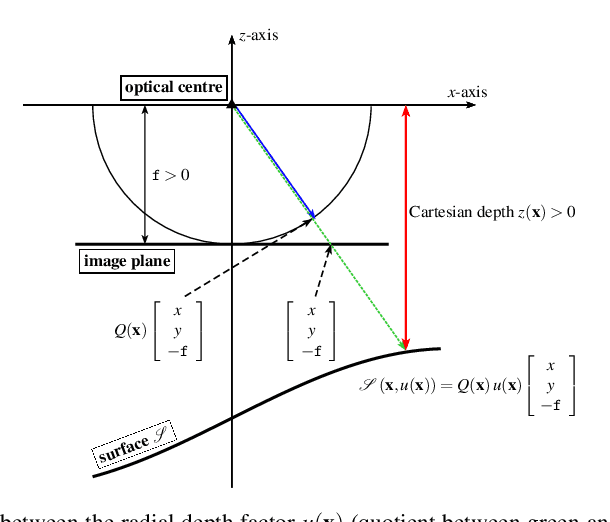
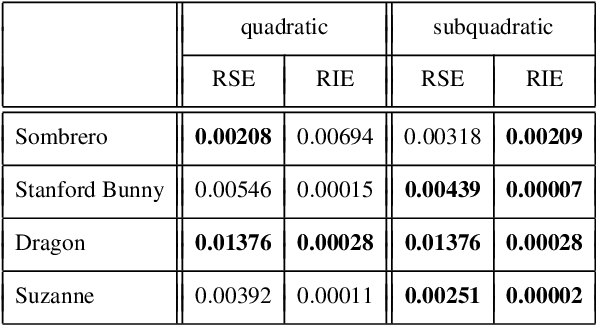
Most of today's state-of-the-art methods for perspective shape from shading are modelled in terms of partial differential equations (PDEs) of Hamilton-Jacobi type. To improve the robustness of such methods w.r.t. noise and missing data, first approaches have recently been proposed that seek to embed the underlying PDE into a variational framework with data and smoothness term. So far, however, such methods either make use of a radial depth parametrisation that makes the regularisation hard to interpret from a geometrical viewpoint or they consider indirect smoothness terms that require additional consistency constraints to provide valid solutions. Moreover the minimisation of such frameworks is an intricate task, since the underlying energy is typically non-convex. In our paper we address all three of the aforementioned issues. First, we propose a novel variational model that operates directly on the Cartesian depth. In this context, we also point out a common mistake in the derivation of the surface normal. Moreover, we employ a direct second-order regulariser with edge-preservation property. This direct regulariser yields by construction valid solutions without requiring additional consistency constraints. Finally, we also propose a novel coarse-to-fine minimisation framework based on an alternating explicit scheme. This framework allows us to avoid local minima during the minimisation and thus to improve the accuracy of the reconstruction. Experiments show the good quality of our model as well as the usefulness of the proposed numerical scheme.