Direct Variational Perspective Shape from Shading with Cartesian Depth Parametrisation
Paper and Code
Jul 13, 2015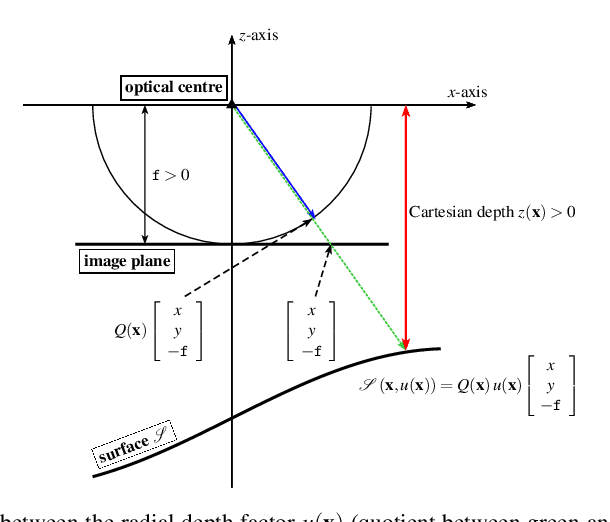

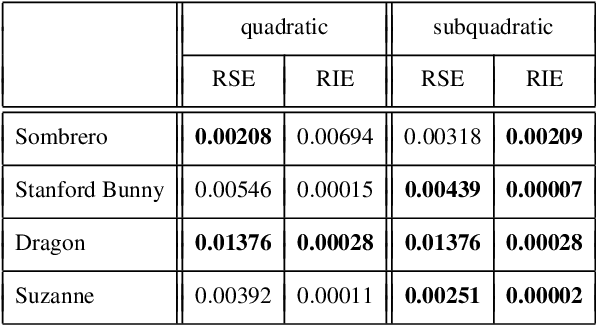
Most of today's state-of-the-art methods for perspective shape from shading are modelled in terms of partial differential equations (PDEs) of Hamilton-Jacobi type. To improve the robustness of such methods w.r.t. noise and missing data, first approaches have recently been proposed that seek to embed the underlying PDE into a variational framework with data and smoothness term. So far, however, such methods either make use of a radial depth parametrisation that makes the regularisation hard to interpret from a geometrical viewpoint or they consider indirect smoothness terms that require additional consistency constraints to provide valid solutions. Moreover the minimisation of such frameworks is an intricate task, since the underlying energy is typically non-convex. In our paper we address all three of the aforementioned issues. First, we propose a novel variational model that operates directly on the Cartesian depth. In this context, we also point out a common mistake in the derivation of the surface normal. Moreover, we employ a direct second-order regulariser with edge-preservation property. This direct regulariser yields by construction valid solutions without requiring additional consistency constraints. Finally, we also propose a novel coarse-to-fine minimisation framework based on an alternating explicit scheme. This framework allows us to avoid local minima during the minimisation and thus to improve the accuracy of the reconstruction. Experiments show the good quality of our model as well as the usefulness of the proposed numerical scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge