Matching the Statistical Query Lower Bound for k-sparse Parity Problems with Stochastic Gradient Descent

The $k$-parity problem is a classical problem in computational complexity and algorithmic theory, serving as a key benchmark for understanding computational classes. In this paper, we solve the $k$-parity problem with stochastic gradient descent (SGD) on two-layer fully-connected neural networks. We demonstrate that SGD can efficiently solve the $k$-sparse parity problem on a $d$-dimensional hypercube ($k\le O(\sqrt{d})$) with a sample complexity of $\tilde{O}(d^{k-1})$ using $2^{\Theta(k)}$ neurons, thus matching the established $\Omega(d^{k})$ lower bounds of Statistical Query (SQ) models. Our theoretical analysis begins by constructing a good neural network capable of correctly solving the $k$-parity problem. We then demonstrate how a trained neural network with SGD can effectively approximate this good network, solving the $k$-parity problem with small statistical errors. Our theoretical results and findings are supported by empirical evidence, showcasing the efficiency and efficacy of our approach.

Guided Discrete Diffusion for Electronic Health Record Generation

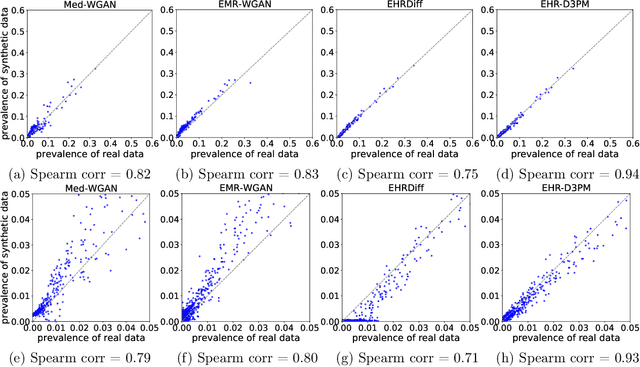
Electronic health records (EHRs) are a pivotal data source that enables numerous applications in computational medicine, e.g., disease progression prediction, clinical trial design, and health economics and outcomes research. Despite wide usability, their sensitive nature raises privacy and confidentially concerns, which limit potential use cases. To tackle these challenges, we explore the use of generative models to synthesize artificial, yet realistic EHRs. While diffusion-based methods have recently demonstrated state-of-the-art performance in generating other data modalities and overcome the training instability and mode collapse issues that plague previous GAN-based approaches, their applications in EHR generation remain underexplored. The discrete nature of tabular medical code data in EHRs poses challenges for high-quality data generation, especially for continuous diffusion models. To this end, we introduce a novel tabular EHR generation method, EHR-D3PM, which enables both unconditional and conditional generation using the discrete diffusion model. Our experiments demonstrate that EHR-D3PM significantly outperforms existing generative baselines on comprehensive fidelity and utility metrics while maintaining less membership vulnerability risks. Furthermore, we show EHR-D3PM is effective as a data augmentation method and enhances performance on downstream tasks when combined with real data.

Fast Sampling via De-randomization for Discrete Diffusion Models

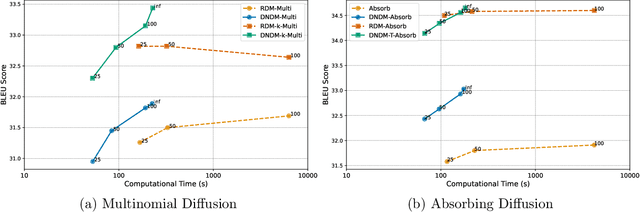
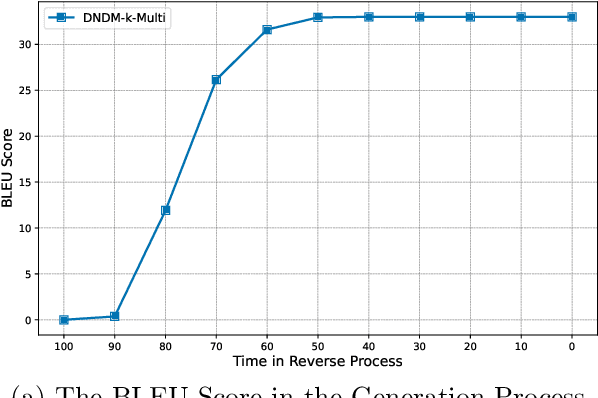
Diffusion models have emerged as powerful tools for high-quality data generation, such as image generation. Despite its success in continuous spaces, discrete diffusion models, which apply to domains such as texts and natural languages, remain under-studied and often suffer from slow generation speed. In this paper, we propose a novel de-randomized diffusion process, which leads to an accelerated algorithm for discrete diffusion models. Our technique significantly reduces the number of function evaluations (i.e., calls to the neural network), making the sampling process much faster. Furthermore, we introduce a continuous-time (i.e., infinite-step) sampling algorithm that can provide even better sample qualities than its discrete-time (finite-step) counterpart. Extensive experiments on natural language generation and machine translation tasks demonstrate the superior performance of our method in terms of both generation speed and sample quality over existing methods for discrete diffusion models.

Implicit Bias of Gradient Descent for Two-layer ReLU and Leaky ReLU Networks on Nearly-orthogonal Data

The implicit bias towards solutions with favorable properties is believed to be a key reason why neural networks trained by gradient-based optimization can generalize well. While the implicit bias of gradient flow has been widely studied for homogeneous neural networks (including ReLU and leaky ReLU networks), the implicit bias of gradient descent is currently only understood for smooth neural networks. Therefore, implicit bias in non-smooth neural networks trained by gradient descent remains an open question. In this paper, we aim to answer this question by studying the implicit bias of gradient descent for training two-layer fully connected (leaky) ReLU neural networks. We showed that when the training data are nearly-orthogonal, for leaky ReLU activation function, gradient descent will find a network with a stable rank that converges to $1$, whereas for ReLU activation function, gradient descent will find a neural network with a stable rank that is upper bounded by a constant. Additionally, we show that gradient descent will find a neural network such that all the training data points have the same normalized margin asymptotically. Experiments on both synthetic and real data backup our theoretical findings.

Why Does Sharpness-Aware Minimization Generalize Better Than SGD?

The challenge of overfitting, in which the model memorizes the training data and fails to generalize to test data, has become increasingly significant in the training of large neural networks. To tackle this challenge, Sharpness-Aware Minimization (SAM) has emerged as a promising training method, which can improve the generalization of neural networks even in the presence of label noise. However, a deep understanding of how SAM works, especially in the setting of nonlinear neural networks and classification tasks, remains largely missing. This paper fills this gap by demonstrating why SAM generalizes better than Stochastic Gradient Descent (SGD) for a certain data model and two-layer convolutional ReLU networks. The loss landscape of our studied problem is nonsmooth, thus current explanations for the success of SAM based on the Hessian information are insufficient. Our result explains the benefits of SAM, particularly its ability to prevent noise learning in the early stages, thereby facilitating more effective learning of features. Experiments on both synthetic and real data corroborate our theory.

Benign Overfitting for Two-layer ReLU Networks

Modern deep learning models with great expressive power can be trained to overfit the training data but still generalize well. This phenomenon is referred to as benign overfitting. Recently, a few studies have attempted to theoretically understand benign overfitting in neural networks. However, these works are either limited to neural networks with smooth activation functions or to the neural tangent kernel regime. How and when benign overfitting can occur in ReLU neural networks remains an open problem. In this work, we seek to answer this question by establishing algorithm-dependent risk bounds for learning two-layer ReLU convolutional neural networks with label-flipping noise. We show that, under mild conditions, the neural network trained by gradient descent can achieve near-zero training loss and Bayes optimal test risk. Our result also reveals a sharp transition between benign and harmful overfitting under different conditions on data distribution in terms of test risk. Experiments on synthetic data back up our theory.