Dynamic Residual Safe Reinforcement Learning for Multi-Agent Safety-Critical Scenarios Decision-Making

In multi-agent safety-critical scenarios, traditional autonomous driving frameworks face significant challenges in balancing safety constraints and task performance. These frameworks struggle to quantify dynamic interaction risks in real-time and depend heavily on manual rules, resulting in low computational efficiency and conservative strategies. To address these limitations, we propose a Dynamic Residual Safe Reinforcement Learning (DRS-RL) framework grounded in a safety-enhanced networked Markov decision process. It's the first time that the weak-to-strong theory is introduced into multi-agent decision-making, enabling lightweight dynamic calibration of safety boundaries via a weak-to-strong safety correction paradigm. Based on the multi-agent dynamic conflict zone model, our framework accurately captures spatiotemporal coupling risks among heterogeneous traffic participants and surpasses the static constraints of conventional geometric rules. Moreover, a risk-aware prioritized experience replay mechanism mitigates data distribution bias by mapping risk to sampling probability. Experimental results reveal that the proposed method significantly outperforms traditional RL algorithms in safety, efficiency, and comfort. Specifically, it reduces the collision rate by up to 92.17%, while the safety model accounts for merely 27% of the main model's parameters.

Generalized Laplace Approximation

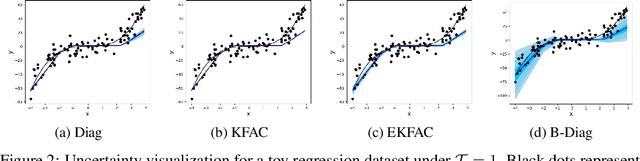
In recent years, the inconsistency in Bayesian deep learning has garnered increasing attention. Tempered or generalized posterior distributions often offer a direct and effective solution to this issue. However, understanding the underlying causes and evaluating the effectiveness of generalized posteriors remain active areas of research. In this study, we introduce a unified theoretical framework to attribute Bayesian inconsistency to model misspecification and inadequate priors. We interpret the generalization of the posterior with a temperature factor as a correction for misspecified models through adjustments to the joint probability model, and the recalibration of priors by redistributing probability mass on models within the hypothesis space using data samples. Additionally, we highlight a distinctive feature of Laplace approximation, which ensures that the generalized normalizing constant can be treated as invariant, unlike the typical scenario in general Bayesian learning where this constant varies with model parameters post-generalization. Building on this insight, we propose the generalized Laplace approximation, which involves a simple adjustment to the computation of the Hessian matrix of the regularized loss function. This method offers a flexible and scalable framework for obtaining high-quality posterior distributions. We assess the performance and properties of the generalized Laplace approximation on state-of-the-art neural networks and real-world datasets.