Multinomial Logit Bandit with Low Switching Cost

We study multinomial logit bandit with limited adaptivity, where the algorithms change their exploration actions as infrequently as possible when achieving almost optimal minimax regret. We propose two measures of adaptivity: the assortment switching cost and the more fine-grained item switching cost. We present an anytime algorithm (AT-DUCB) with $O(N \log T)$ assortment switches, almost matching the lower bound $\Omega(\frac{N \log T}{ \log \log T})$. In the fixed-horizon setting, our algorithm FH-DUCB incurs $O(N \log \log T)$ assortment switches, matching the asymptotic lower bound. We also present the ESUCB algorithm with item switching cost $O(N \log^2 T)$.

Stochastic Linear Optimization with Adversarial Corruption

We extend the model of stochastic bandits with adversarial corruption (Lykouriset al., 2018) to the stochastic linear optimization problem (Dani et al., 2008). Our algorithm is agnostic to the amount of corruption chosen by the adaptive adversary. The regret of the algorithm only increases linearly in the amount of corruption. Our algorithm involves using L\"owner-John's ellipsoid for exploration and dividing time horizon into epochs with exponentially increasing size to limit the influence of corruption.

Tight Regret Bounds for Infinite-armed Linear Contextual Bandits

Linear contextual bandit is a class of sequential decision making problems with important applications in recommendation systems, online advertising, healthcare, and other machine learning related tasks. While there is much prior research, tight regret bounds of linear contextual bandit with infinite action sets remain open. In this paper, we prove regret upper bound of $O(\sqrt{d^2T\log T})\times \mathrm{poly}(\log\log T)$ where $d$ is the domain dimension and $T$ is the time horizon. Our upper bound matches the previous lower bound of $\Omega(\sqrt{d^2 T\log T})$ up to iterated logarithmic terms.

Nearly Minimax-Optimal Regret for Linearly Parameterized Bandits

We study the linear contextual bandit problem with finite action sets. When the problem dimension is $d$, the time horizon is $T$, and there are $n \leq 2^{d/2}$ candidate actions per time period, we (1) show that the minimax expected regret is $\Omega(\sqrt{dT \log T \log n})$ for every algorithm, and (2) introduce a Variable-Confidence-Level (VCL) SupLinUCB algorithm whose regret matches the lower bound up to iterated logarithmic factors. Our algorithmic result saves two $\sqrt{\log T}$ factors from previous analysis, and our information-theoretical lower bound also improves previous results by one $\sqrt{\log T}$ factor, revealing a regret scaling quite different from classical multi-armed bandits in which no logarithmic $T$ term is present in minimax regret. Our proof techniques include variable confidence levels and a careful analysis of layer sizes of SupLinUCB on the upper bound side, and delicately constructed adversarial sequences showing the tightness of elliptical potential lemmas on the lower bound side.

Implementation of Stochastic Quasi-Newton's Method in PyTorch

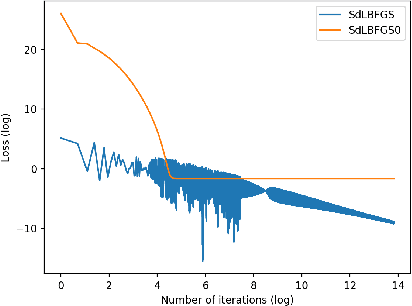
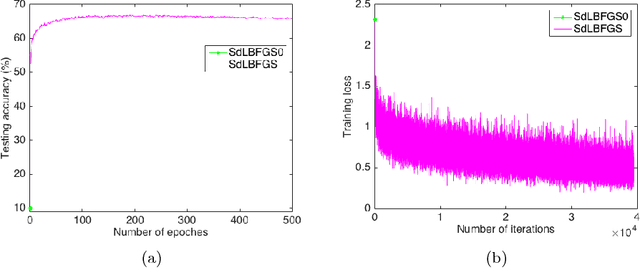
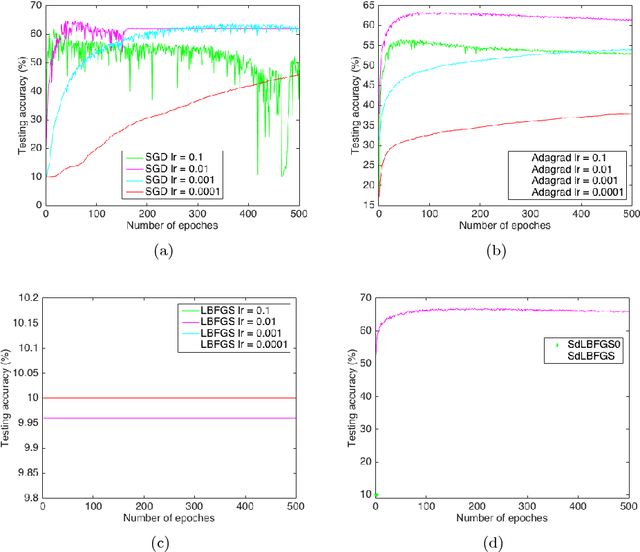
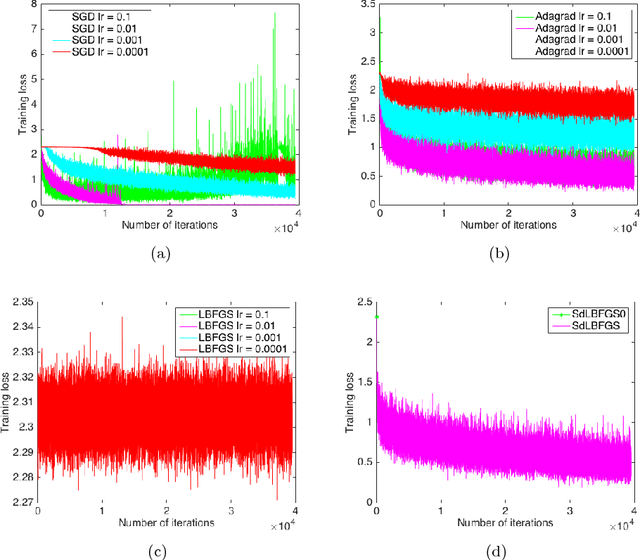
In this paper, we implement the Stochastic Damped LBFGS (SdLBFGS) for stochastic non-convex optimization. We make two important modifications to the original SdLBFGS algorithm. First, by initializing the Hessian at each step using an identity matrix, the algorithm converges better than original algorithm. Second, by performing direction normalization we could gain stable optimization procedure without line search. Experiments on minimizing a 2D non-convex function shows that our improved algorithm converges better than original algorithm, and experiments on the CIFAR10 and MNIST datasets show that our improved algorithm works stably and gives comparable or even better testing accuracies than first order optimizers SGD, Adagrad, and second order optimizers LBFGS in PyTorch.