Enhanced Multimodal Hate Video Detection via Channel-wise and Modality-wise Fusion

The rapid rise of video content on platforms such as TikTok and YouTube has transformed information dissemination, but it has also facilitated the spread of harmful content, particularly hate videos. Despite significant efforts to combat hate speech, detecting these videos remains challenging due to their often implicit nature. Current detection methods primarily rely on unimodal approaches, which inadequately capture the complementary features across different modalities. While multimodal techniques offer a broader perspective, many fail to effectively integrate temporal dynamics and modality-wise interactions essential for identifying nuanced hate content. In this paper, we present CMFusion, an enhanced multimodal hate video detection model utilizing a novel Channel-wise and Modality-wise Fusion Mechanism. CMFusion first extracts features from text, audio, and video modalities using pre-trained models and then incorporates a temporal cross-attention mechanism to capture dependencies between video and audio streams. The learned features are then processed by channel-wise and modality-wise fusion modules to obtain informative representations of videos. Our extensive experiments on a real-world dataset demonstrate that CMFusion significantly outperforms five widely used baselines in terms of accuracy, precision, recall, and F1 score. Comprehensive ablation studies and parameter analyses further validate our design choices, highlighting the model's effectiveness in detecting hate videos. The source codes will be made publicly available at https://github.com/EvelynZ10/cmfusion.

A Low-dose CT Reconstruction Network Based on TV-regularized OSEM Algorithm

Low-dose computed tomography (LDCT) offers significant advantages in reducing the potential harm to human bodies. However, reducing the X-ray dose in CT scanning often leads to severe noise and artifacts in the reconstructed images, which might adversely affect diagnosis. By utilizing the expectation maximization (EM) algorithm, statistical priors could be combined with artificial priors to improve LDCT reconstruction quality. However, conventional EM-based regularization methods adopt an alternating solving strategy, i.e. full reconstruction followed by image-regularization, resulting in over-smoothing and slow convergence. In this paper, we propose to integrate TV regularization into the ``M''-step of the EM algorithm, thus achieving effective and efficient regularization. Besides, by employing the Chambolle-Pock (CP) algorithm and the ordered subset (OS) strategy, we propose the OSEM-CP algorithm for LDCT reconstruction, in which both reconstruction and regularization are conducted view-by-view. Furthermore, by unrolling OSEM-CP, we propose an end-to-end reconstruction neural network (NN), named OSEM-CPNN, with remarkable performance and efficiency that achieves high-quality reconstructions in just one full-view iteration. Experiments on different models and datasets demonstrate our methods' outstanding performance compared to traditional and state-of-the-art deep-learning methods.

Learning Order Parameters from Videos of Dynamical Phases for Skyrmions with Neural Networks

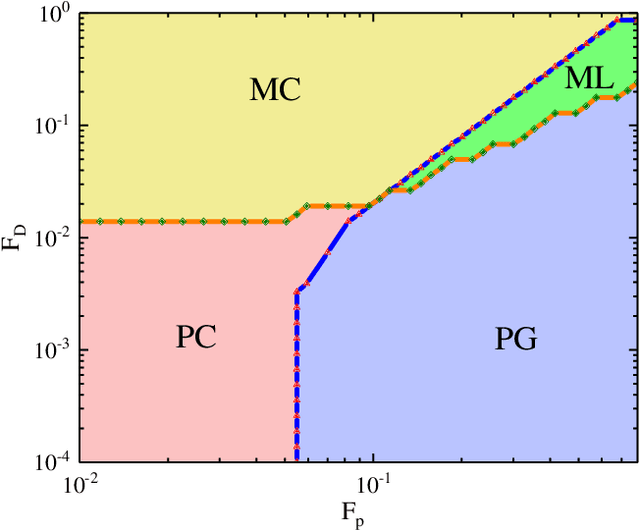
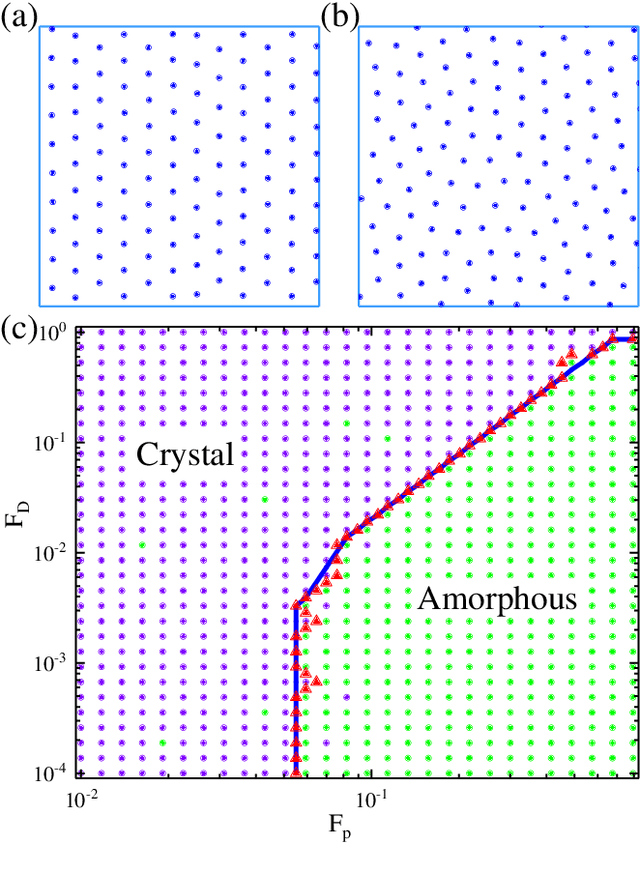
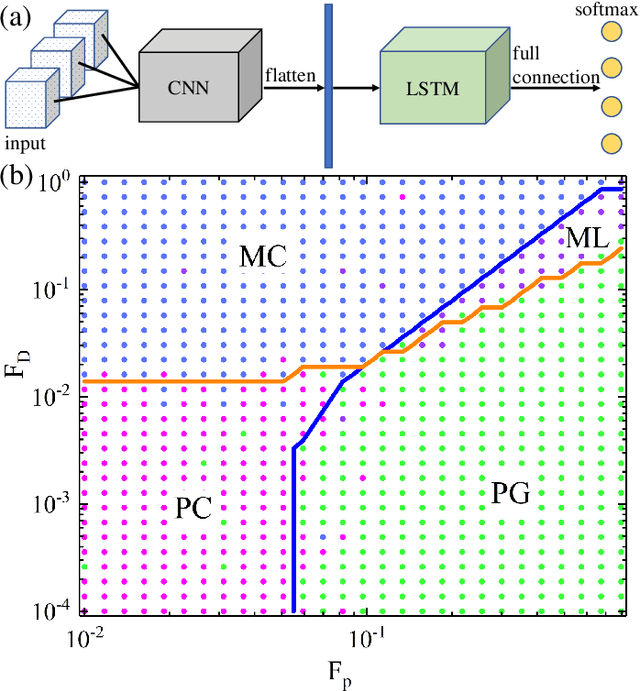
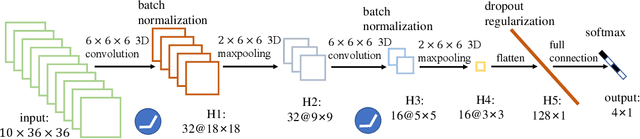
The ability to recognize dynamical phenomena (e.g., dynamical phases) and dynamical processes in physical events from videos, then to abstract physical concepts and reveal physical laws, lies at the core of human intelligence. The main purposes of this paper are to use neural networks for classifying the dynamical phases of some videos and to demonstrate that neural networks can learn physical concepts from them. To this end, we employ multiple neural networks to recognize the static phases (image format) and dynamical phases (video format) of a particle-based skyrmion model. Our results show that neural networks, without any prior knowledge, can not only correctly classify these phases, but also predict the phase boundaries which agree with those obtained by simulation. We further propose a parameter visualization scheme to interpret what neural networks have learned. We show that neural networks can learn two order parameters from videos of dynamical phases and predict the critical values of two order parameters. Finally, we demonstrate that only two order parameters are needed to identify videos of skyrmion dynamical phases. It shows that this parameter visualization scheme can be used to determine how many order parameters are needed to fully recognize the input phases. Our work sheds light on the future use of neural networks in discovering new physical concepts and revealing unknown yet physical laws from videos.

Restricted Linearized Augmented Lagrangian Method for Euler's Elastica Model

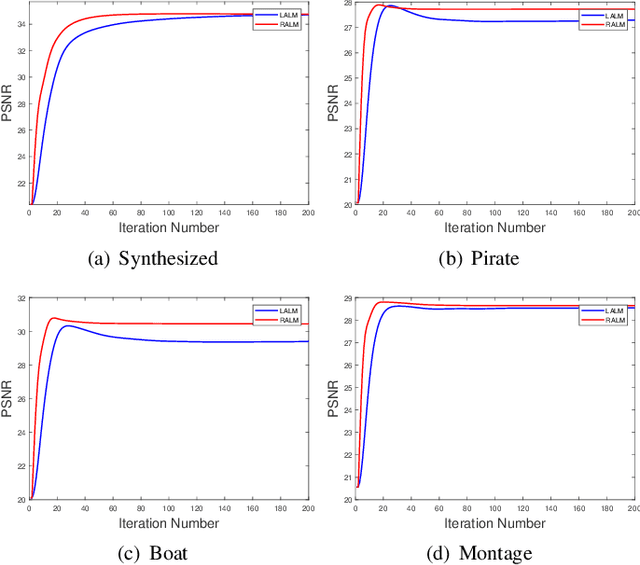
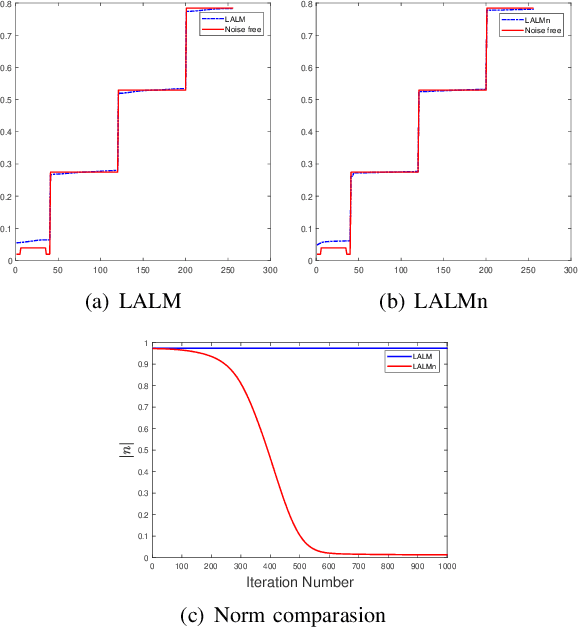
Euler's elastica model has been extensively studied and applied to image processing tasks. However, due to the high nonlinearity and nonconvexity of the involved curvature term, conventional algorithms suffer from slow convergence and high computational cost. Various fast algorithms have been proposed, among which, the augmented Lagrangian based ones are very popular in the community. However, parameter tuning might be very challenging for these methods. In this paper, a simple cutting-off strategy is introduced into the augmented Lagrangian based algorithms for minimizing the Euler's elastica energy, which leads to easy parameter tuning and fast convergence. The cutting-off strategy is based on an observation of inconsistency inside the augmented Lagrangian based algorithms. When the weighting parameter of the curvature term goes to zero, the energy functional boils down to the ROF model. So, a natural requirement is that its augmented Lagrangian based algorithms should also approach the augmented Lagrangian based algorithms formulated directly for solving the ROF model from the very beginning. Unfortunately, this is not the case for certain existing augmented Lagrangian based algorithms. The proposed cutting-off strategy helps to decouple the tricky dependence between the auxiliary splitting variables, so as to remove the observed inconsistency. Numerical experiments suggest that the proposed algorithm enjoys easier parameter-tuning, faster convergence and even higher quality of image restorations.