BLEURT Has Universal Translations: An Analysis of Automatic Metrics by Minimum Risk Training

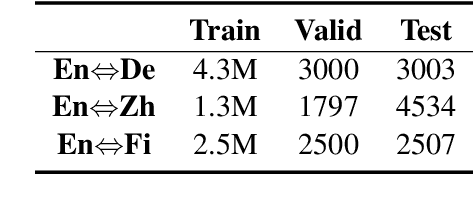
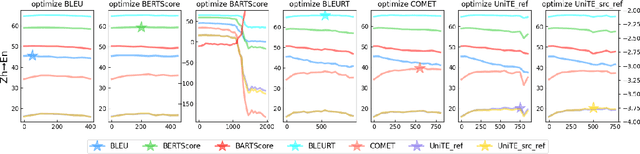
Automatic metrics play a crucial role in machine translation. Despite the widespread use of n-gram-based metrics, there has been a recent surge in the development of pre-trained model-based metrics that focus on measuring sentence semantics. However, these neural metrics, while achieving higher correlations with human evaluations, are often considered to be black boxes with potential biases that are difficult to detect. In this study, we systematically analyze and compare various mainstream and cutting-edge automatic metrics from the perspective of their guidance for training machine translation systems. Through Minimum Risk Training (MRT), we find that certain metrics exhibit robustness defects, such as the presence of universal adversarial translations in BLEURT and BARTScore. In-depth analysis suggests two main causes of these robustness deficits: distribution biases in the training datasets, and the tendency of the metric paradigm. By incorporating token-level constraints, we enhance the robustness of evaluation metrics, which in turn leads to an improvement in the performance of machine translation systems. Codes are available at \url{https://github.com/powerpuffpomelo/fairseq_mrt}.

Amortized Inference of Variational Bounds for Learning Noisy-OR

Classical approaches for approximate inference depend on cleverly designed variational distributions and bounds. Modern approaches employ amortized variational inference, which uses a neural network to approximate any posterior without leveraging the structures of the generative models. In this paper, we propose Amortized Conjugate Posterior (ACP), a hybrid approach taking advantages of both types of approaches. Specifically, we use the classical methods to derive specific forms of posterior distributions and then learn the variational parameters using amortized inference. We study the effectiveness of the proposed approach on the Noisy-OR model and compare to both the classical and the modern approaches for approximate inference and parameter learning. Our results show that ACP outperforms other methods when there is a limited amount of training data.