Yimin D. Zhang
Advancing Single-Snapshot DOA Estimation with Siamese Neural Networks for Sparse Linear Arrays
Jan 13, 2025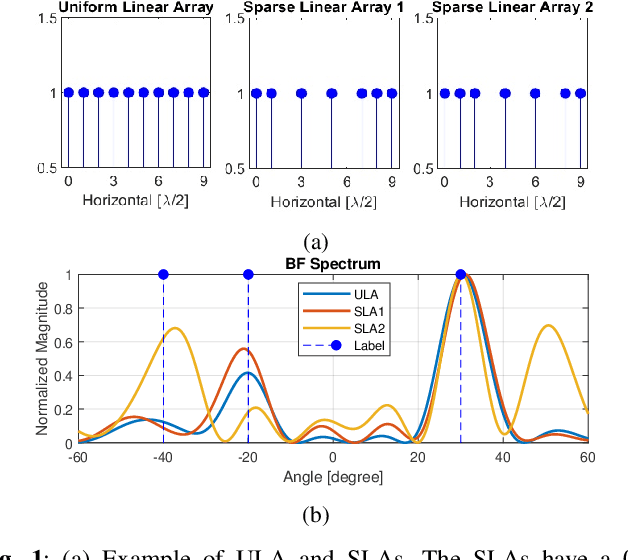
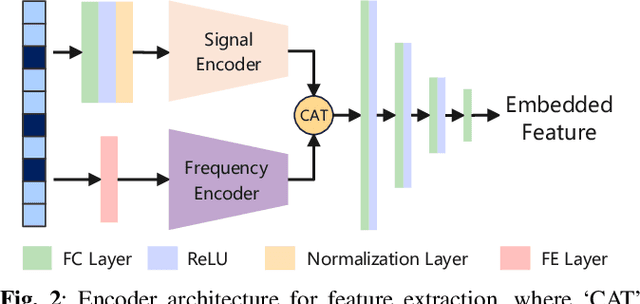
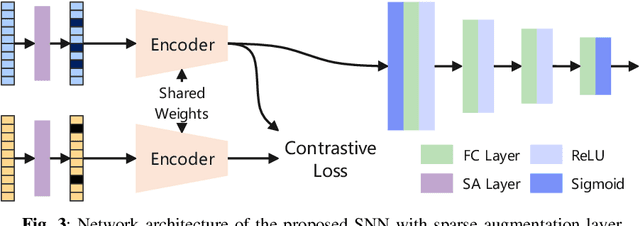
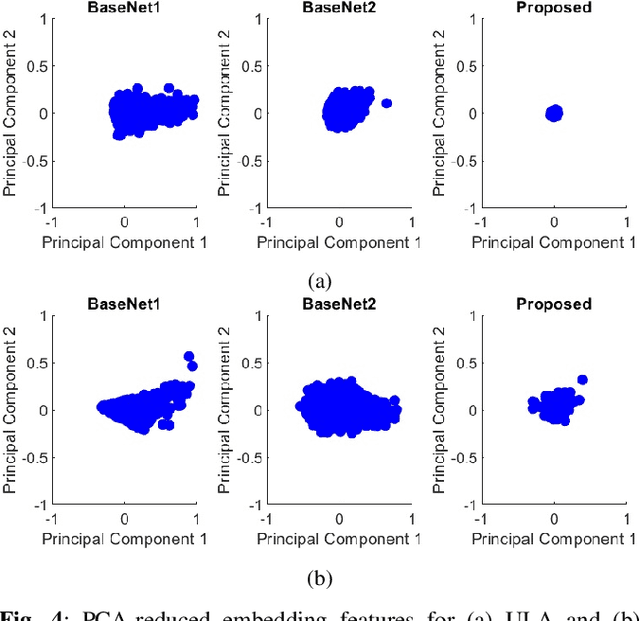
Abstract:Single-snapshot signal processing in sparse linear arrays has become increasingly vital, particularly in dynamic environments like automotive radar systems, where only limited snapshots are available. These arrays are often utilized either to cut manufacturing costs or result from unintended antenna failures, leading to challenges such as high sidelobe levels and compromised accuracy in direction-of-arrival (DOA) estimation. Despite deep learning's success in tasks such as DOA estimation, the need for extensive training data to increase target numbers or improve angular resolution poses significant challenges. In response, this paper presents a novel Siamese neural network (SNN) featuring a sparse augmentation layer, which enhances signal feature embedding and DOA estimation accuracy in sparse arrays. We demonstrate the enhanced DOA estimation performance of our approach through detailed feature analysis and performance evaluation. The code for this study is available at https://github.com/ruxinzh/SNNS_SLA.
Enhancing Off-Grid One-Bit DOA Estimation with Learning-Based Sparse Bayesian Approach for Non-Uniform Sparse Array
Dec 14, 2024
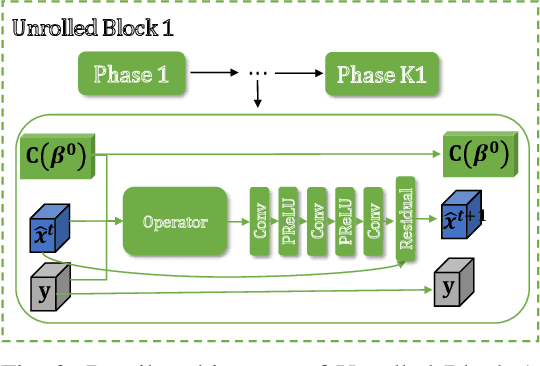
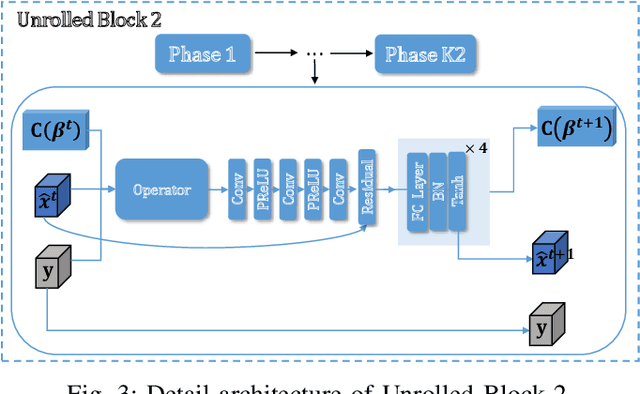
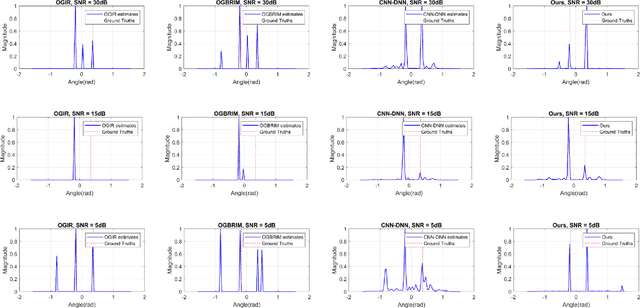
Abstract:This paper tackles the challenge of one-bit off-grid direction of arrival (DOA) estimation in a single snapshot scenario based on a learning-based Bayesian approach. Firstly, we formulate the off-grid DOA estimation model, utilizing the first-order off-grid approximation, incorporating one-bit data quantization. Subsequently, we address this problem using the Sparse Bayesian based framework and solve iteratively. However, traditional Sparse Bayesian methods often face challenges such as high computational complexity and the need for extensive hyperparameter tuning. To balance estimation accuracy and computational efficiency, we propose a novel Learning-based Sparse Bayesian framework, which leverages an unrolled neural network architecture. This framework autonomously learns hyperparameters through supervised learning, offering more accurate off-grid DOA estimates and improved computational efficiency compared to some state-of-the-art methods. Furthermore, the proposed approach is applicable to both uniform linear arrays and non-uniform sparse arrays. Simulation results validate the effectiveness of the proposed framework.
Joint DoA-Range Estimation Using Space-Frequency Virtual Difference Coarray
Apr 15, 2022
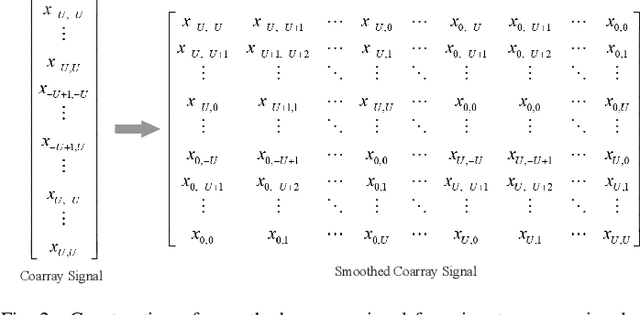
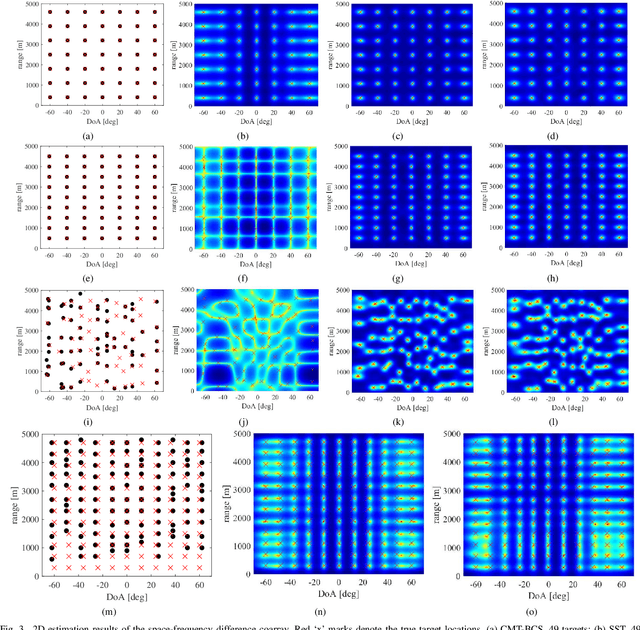
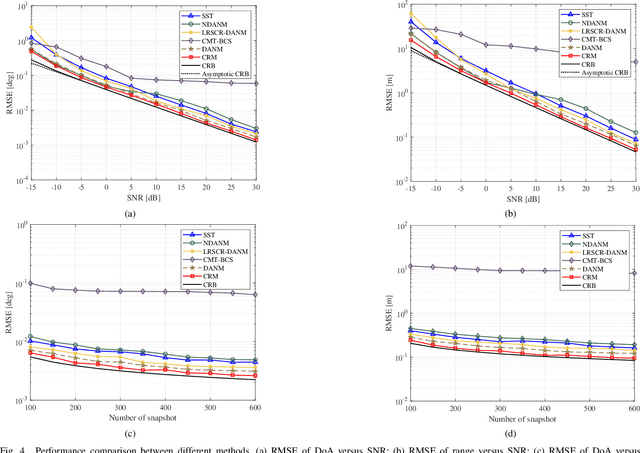
Abstract:In this paper, we address the problem of joint direction-of-arrival (DoA) and range estimation using frequency diverse coprime array (FDCA). By incorporating the coprime array structure and coprime frequency offsets, a two-dimensional space-frequency virtual difference coarray corresponding to uniform array and uniform frequency offset is considered to increase the number of degrees-of-freedom (DoFs). However, the reconstruction of the doubly-Toeplitz covariance matrix is computationally prohibitive. To solve this problem, we propose an interpolation algorithm based on decoupled atomic norm minimization (DANM), which converts the coarray signal to a simple matrix form. On this basis, a relaxation-based optimization problem is formulated to achieve joint DoA-range estimation with enhanced DoFs. The reconstructed coarray signal enables application of existing subspace-based spectral estimation methods. The proposed DANM problem is further reformulated as an equivalent rank-minimization problem which is solved by cyclic rank minimization. This approach avoids the approximation errors introduced in nuclear norm-based approach, thereby achieving superior root-mean-square error which is closer to the Cramer-Rao bound. The effectiveness of proposed method is confirmed by theoretical analyses and numerical simulations.
Rank Minimization-based Toeplitz Reconstruction for DoA Estimation Using Coprime Array
Mar 29, 2021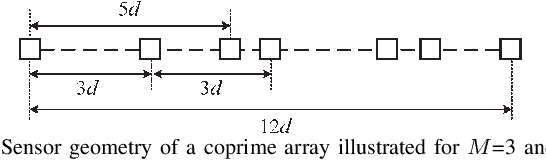
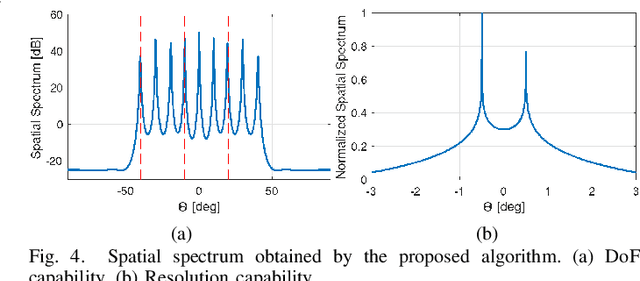

Abstract:In this paper, we address the problem of direction finding using coprime array, which is one of the most preferred sparse array configurations. Motivated by the fact that non-uniform element spacing hinders full utilization of the underlying information in the receive signals, we propose a direction-of-arrival (DoA) estimation algorithm based on low-rank reconstruction of the Toeplitz covariance matrix. The atomic-norm representation of the measurements from the interpolated virtual array is considered, and the equivalent dual-variable rank minimization problem is formulated and solved using a cyclic optimization approach. The recovered covariance matrix enables the application of conventional subspace-based spectral estimation algorithms, such as MUSIC, to achieve enhanced DoA estimation performance. The estimation performance of the proposed approach, in terms of the degrees-of-freedom and spatial resolution, is examined. We also show the superiority of the proposed method over the competitive approaches in the root-mean-square error sense.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge