On the Superlinear Relationship between SGD Noise Covariance and Loss Landscape Curvature

Stochastic Gradient Descent (SGD) introduces anisotropic noise that is correlated with the local curvature of the loss landscape, thereby biasing optimization toward flat minima. Prior work often assumes an equivalence between the Fisher Information Matrix and the Hessian for negative log-likelihood losses, leading to the claim that the SGD noise covariance $\mathbf{C}$ is proportional to the Hessian $\mathbf{H}$. We show that this assumption holds only under restrictive conditions that are typically violated in deep neural networks. Using the recently discovered Activity--Weight Duality, we find a more general relationship agnostic to the specific loss formulation, showing that $\mathbf{C} \propto \mathbb{E}_p[\mathbf{h}_p^2]$, where $\mathbf{h}_p$ denotes the per-sample Hessian with $\mathbf{H} = \mathbb{E}_p[\mathbf{h}_p]$. As a consequence, $\mathbf{C}$ and $\mathbf{H}$ commute approximately rather than coincide exactly, and their diagonal elements follow an approximate power-law relation $C_{ii} \propto H_{ii}^γ$ with a theoretically bounded exponent $1 \leq γ\leq 2$, determined by per-sample Hessian spectra. Experiments across datasets, architectures, and loss functions validate these bounds, providing a unified characterization of the noise-curvature relationship in deep learning.

Transient learning dynamics drive escape from sharp valleys in Stochastic Gradient Descent

Stochastic gradient descent (SGD) is central to deep learning, yet the dynamical origin of its preference for flatter, more generalizable solutions remains unclear. Here, by analyzing SGD learning dynamics, we identify a nonequilibrium mechanism governing solution selection. Numerical experiments reveal a transient exploratory phase in which SGD trajectories repeatedly escape sharp valleys and transition toward flatter regions of the loss landscape. By using a tractable physical model, we show that the SGD noise reshapes the landscape into an effective potential that favors flat solutions. Crucially, we uncover a transient freezing mechanism: as training proceeds, growing energy barriers suppress inter-valley transitions and ultimately trap the dynamics within a single basin. Increasing the SGD noise strength delays this freezing, which enhances convergence to flatter minima. Together, these results provide a unified physical framework linking learning dynamics, loss-landscape geometry, and generalization, and suggest principles for the design of more effective optimization algorithms.

GPNet: Simplifying Graph Neural Networks via Multi-channel Geometric Polynomials

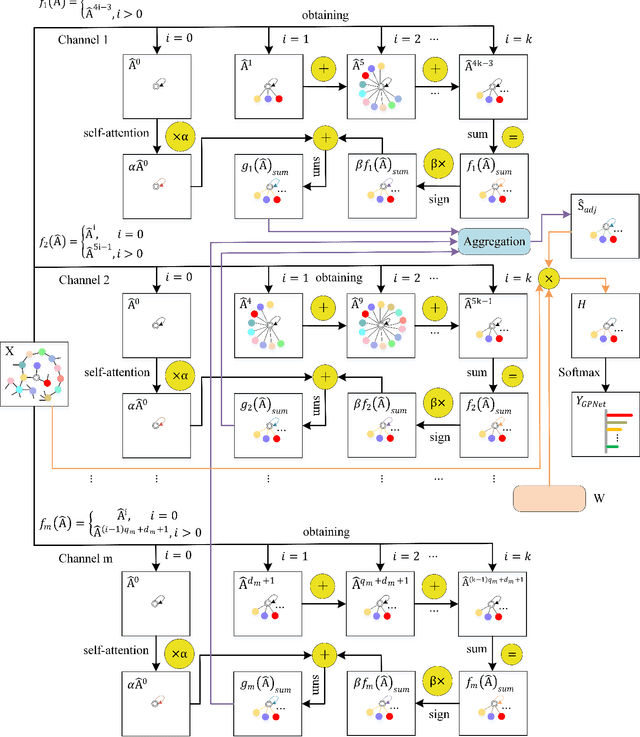
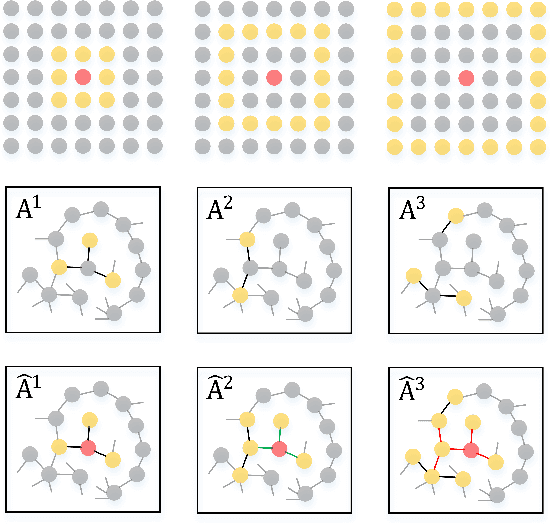
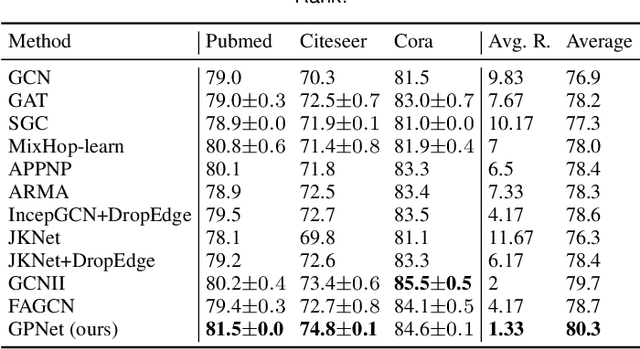
Graph Neural Networks (GNNs) are a promising deep learning approach for circumventing many real-world problems on graph-structured data. However, these models usually have at least one of four fundamental limitations: over-smoothing, over-fitting, difficult to train, and strong homophily assumption. For example, Simple Graph Convolution (SGC) is known to suffer from the first and fourth limitations. To tackle these limitations, we identify a set of key designs including (D1) dilated convolution, (D2) multi-channel learning, (D3) self-attention score, and (D4) sign factor to boost learning from different types (i.e. homophily and heterophily) and scales (i.e. small, medium, and large) of networks, and combine them into a graph neural network, GPNet, a simple and efficient one-layer model. We theoretically analyze the model and show that it can approximate various graph filters by adjusting the self-attention score and sign factor. Experiments show that GPNet consistently outperforms baselines in terms of average rank, average accuracy, complexity, and parameters on semi-supervised and full-supervised tasks, and achieves competitive performance compared to state-of-the-art model with inductive learning task.