mFabric: An Efficient and Scalable Fabric for Mixture-of-Experts Training

Mixture-of-Expert (MoE) models outperform conventional models by selectively activating different subnets, named \emph{experts}, on a per-token basis. This gated computation generates dynamic communications that cannot be determined beforehand, challenging the existing GPU interconnects that remain \emph{static} during the distributed training process. In this paper, we advocate for a first-of-its-kind system, called mFabric, that unlocks topology reconfiguration \emph{during} distributed MoE training. Towards this vision, we first perform a production measurement study and show that the MoE dynamic communication pattern has \emph{strong locality}, alleviating the requirement of global reconfiguration. Based on this, we design and implement a \emph{regionally reconfigurable high-bandwidth domain} on top of existing electrical interconnects using optical circuit switching (OCS), achieving scalability while maintaining rapid adaptability. We have built a fully functional mFabric prototype with commodity hardware and a customized collective communication runtime that trains state-of-the-art MoE models with \emph{in-training} topology reconfiguration across 32 A100 GPUs. Large-scale packet-level simulations show that mFabric delivers comparable performance as the non-blocking fat-tree fabric while boosting the training cost efficiency (e.g., performance per dollar) of four representative MoE models by 1.2$\times$--1.5$\times$ and 1.9$\times$--2.3$\times$ at 100 Gbps and 400 Gbps link bandwidths, respectively.

A Novel Regularized Principal Graph Learning Framework on Explicit Graph Representation

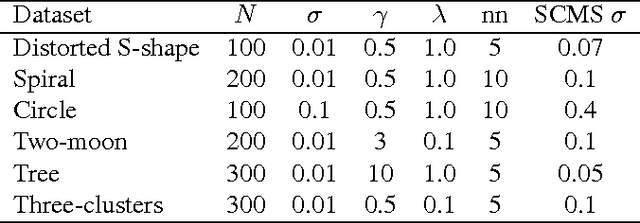
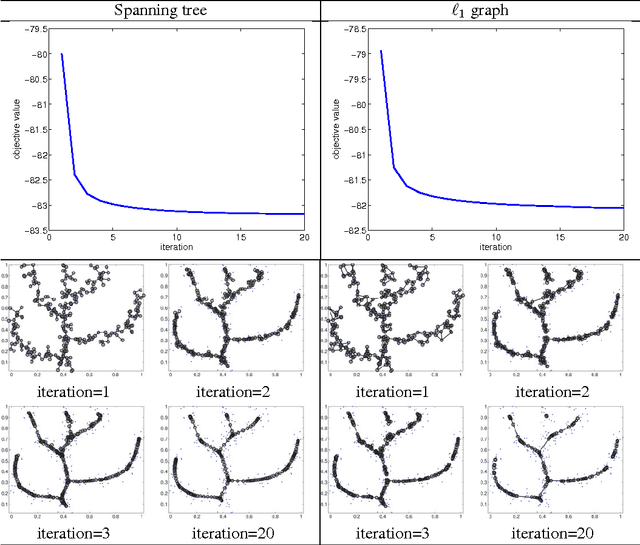
Many scientific datasets are of high dimension, and the analysis usually requires visual manipulation by retaining the most important structures of data. Principal curve is a widely used approach for this purpose. However, many existing methods work only for data with structures that are not self-intersected, which is quite restrictive for real applications. A few methods can overcome the above problem, but they either require complicated human-made rules for a specific task with lack of convergence guarantee and adaption flexibility to different tasks, or cannot obtain explicit structures of data. To address these issues, we develop a new regularized principal graph learning framework that captures the local information of the underlying graph structure based on reversed graph embedding. As showcases, models that can learn a spanning tree or a weighted undirected $\ell_1$ graph are proposed, and a new learning algorithm is developed that learns a set of principal points and a graph structure from data, simultaneously. The new algorithm is simple with guaranteed convergence. We then extend the proposed framework to deal with large-scale data. Experimental results on various synthetic and six real world datasets show that the proposed method compares favorably with baselines and can uncover the underlying structure correctly.