Interpretable Multimodal Learning for Tumor Protein-Metal Binding: Progress, Challenges, and Perspectives

In cancer therapeutics, protein-metal binding mechanisms critically govern drug pharmacokinetics and targeting efficacy, thereby fundamentally shaping the rational design of anticancer metallodrugs. While conventional laboratory methods used to study such mechanisms are often costly, low throughput, and limited in capturing dynamic biological processes, machine learning (ML) has emerged as a promising alternative. Despite increasing efforts to develop protein-metal binding datasets and ML algorithms, the application of ML in tumor protein-metal binding remains limited. Key challenges include a shortage of high-quality, tumor-specific datasets, insufficient consideration of multiple data modalities, and the complexity of interpreting results due to the ''black box'' nature of complex ML models. This paper summarizes recent progress and ongoing challenges in using ML to predict tumor protein-metal binding, focusing on data, modeling, and interpretability. We present multimodal protein-metal binding datasets and outline strategies for acquiring, curating, and preprocessing them for training ML models. Moreover, we explore the complementary value provided by different data modalities and examine methods for their integration. We also review approaches for improving model interpretability to support more trustworthy decisions in cancer research. Finally, we offer our perspective on research opportunities and propose strategies to address the scarcity of tumor protein data and the limited number of predictive models for tumor protein-metal binding. We also highlight two promising directions for effective metal-based drug design: integrating protein-protein interaction data to provide structural insights into metal-binding events and predicting structural changes in tumor proteins after metal binding.

Asynchronous Parallel Stochastic Gradient for Nonconvex Optimization

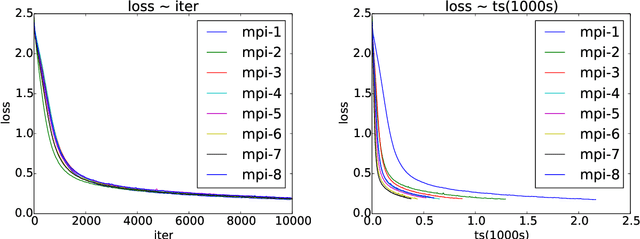
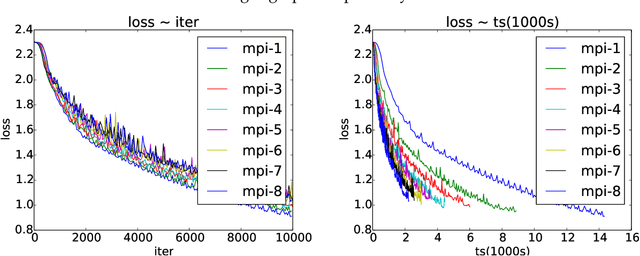
Asynchronous parallel implementations of stochastic gradient (SG) have been broadly used in solving deep neural network and received many successes in practice recently. However, existing theories cannot explain their convergence and speedup properties, mainly due to the nonconvexity of most deep learning formulations and the asynchronous parallel mechanism. To fill the gaps in theory and provide theoretical supports, this paper studies two asynchronous parallel implementations of SG: one is on the computer network and the other is on the shared memory system. We establish an ergodic convergence rate $O(1/\sqrt{K})$ for both algorithms and prove that the linear speedup is achievable if the number of workers is bounded by $\sqrt{K}$ ($K$ is the total number of iterations). Our results generalize and improve existing analysis for convex minimization.

Exclusive Sparsity Norm Minimization with Random Groups via Cone Projection

Many practical applications such as gene expression analysis, multi-task learning, image recognition, signal processing, and medical data analysis pursue a sparse solution for the feature selection purpose and particularly favor the nonzeros \emph{evenly} distributed in different groups. The exclusive sparsity norm has been widely used to serve to this purpose. However, it still lacks systematical studies for exclusive sparsity norm optimization. This paper offers two main contributions from the optimization perspective: 1) We provide several efficient algorithms to solve exclusive sparsity norm minimization with either smooth loss or hinge loss (non-smooth loss). All algorithms achieve the optimal convergence rate $O(1/k^2)$ ($k$ is the iteration number). To the best of our knowledge, this is the first time to guarantee such convergence rate for the general exclusive sparsity norm minimization; 2) When the group information is unavailable to define the exclusive sparsity norm, we propose to use the random grouping scheme to construct groups and prove that if the number of groups is appropriately chosen, the nonzeros (true features) would be grouped in the ideal way with high probability. Empirical studies validate the efficiency of proposed algorithms, and the effectiveness of random grouping scheme on the proposed exclusive SVM formulation.