TSPRank: Bridging Pairwise and Listwise Methods with a Bilinear Travelling Salesman Model

Traditional Learning-To-Rank (LETOR) approaches, including pairwise methods like RankNet and LambdaMART, often fall short by solely focusing on pairwise comparisons, leading to sub-optimal global rankings. Conversely, deep learning based listwise methods, while aiming to optimise entire lists, require complex tuning and yield only marginal improvements over robust pairwise models. To overcome these limitations, we introduce Travelling Salesman Problem Rank (TSPRank), a hybrid pairwise-listwise ranking method. TSPRank reframes the ranking problem as a Travelling Salesman Problem (TSP), a well-known combinatorial optimisation challenge that has been extensively studied for its numerous solution algorithms and applications. This approach enables the modelling of pairwise relationships and leverages combinatorial optimisation to determine the listwise ranking. This approach can be directly integrated as an additional component into embeddings generated by existing backbone models to enhance ranking performance. Our extensive experiments across three backbone models on diverse tasks, including stock ranking, information retrieval, and historical events ordering, demonstrate that TSPRank significantly outperforms both pure pairwise and listwise methods. Our qualitative analysis reveals that TSPRank's main advantage over existing methods is its ability to harness global information better while ranking. TSPRank's robustness and superior performance across different domains highlight its potential as a versatile and effective LETOR solution. The code and preprocessed data are available at https://github.com/waylonli/TSPRank-KDD2025.

Discrete Choice Analysis with Machine Learning Capabilities

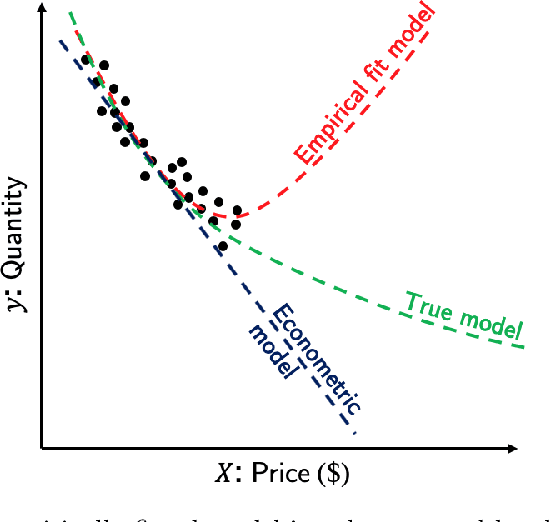
This paper discusses capabilities that are essential to models applied in policy analysis settings and the limitations of direct applications of off-the-shelf machine learning methodologies to such settings. Traditional econometric methodologies for building discrete choice models for policy analysis involve combining data with modeling assumptions guided by subject-matter considerations. Such considerations are typically most useful in specifying the systematic component of random utility discrete choice models but are typically of limited aid in determining the form of the random component. We identify an area where machine learning paradigms can be leveraged, namely in specifying and systematically selecting the best specification of the random component of the utility equations. We review two recent novel applications where mixed-integer optimization and cross-validation are used to algorithmically select optimal specifications for the random utility components of nested logit and logit mixture models subject to interpretability constraints.

Sparse Covariance Estimation in Logit Mixture Models

This paper introduces a new data-driven methodology for estimating sparse covariance matrices of the random coefficients in logit mixture models. Researchers typically specify covariance matrices in logit mixture models under one of two extreme assumptions: either an unrestricted full covariance matrix (allowing correlations between all random coefficients), or a restricted diagonal matrix (allowing no correlations at all). Our objective is to find optimal subsets of correlated coefficients for which we estimate covariances. We propose a new estimator, called MISC, that uses a mixed-integer optimization (MIO) program to find an optimal block diagonal structure specification for the covariance matrix, corresponding to subsets of correlated coefficients, for any desired sparsity level using Markov Chain Monte Carlo (MCMC) posterior draws from the unrestricted full covariance matrix. The optimal sparsity level of the covariance matrix is determined using out-of-sample validation. We demonstrate the ability of MISC to correctly recover the true covariance structure from synthetic data. In an empirical illustration using a stated preference survey on modes of transportation, we use MISC to obtain a sparse covariance matrix indicating how preferences for attributes are related to one another.