Discrete Choice Analysis with Machine Learning Capabilities

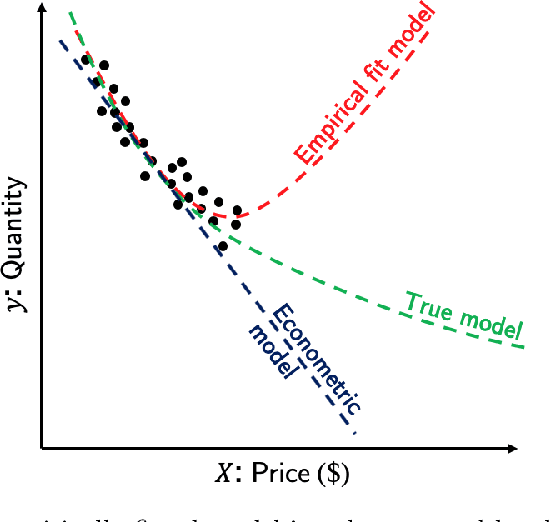
This paper discusses capabilities that are essential to models applied in policy analysis settings and the limitations of direct applications of off-the-shelf machine learning methodologies to such settings. Traditional econometric methodologies for building discrete choice models for policy analysis involve combining data with modeling assumptions guided by subject-matter considerations. Such considerations are typically most useful in specifying the systematic component of random utility discrete choice models but are typically of limited aid in determining the form of the random component. We identify an area where machine learning paradigms can be leveraged, namely in specifying and systematically selecting the best specification of the random component of the utility equations. We review two recent novel applications where mixed-integer optimization and cross-validation are used to algorithmically select optimal specifications for the random utility components of nested logit and logit mixture models subject to interpretability constraints.

Learning Structure in Nested Logit Models

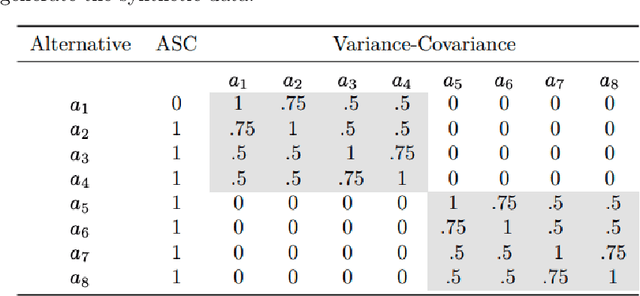
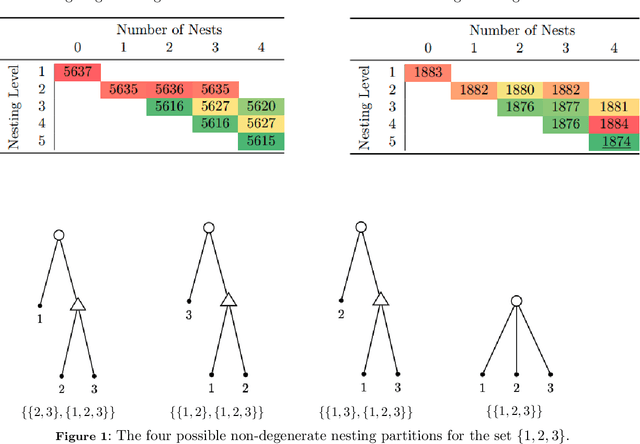
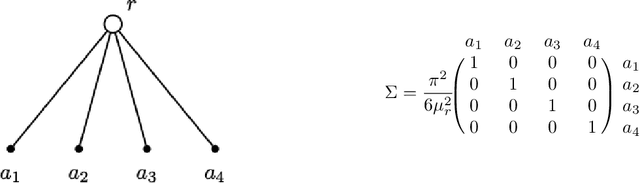
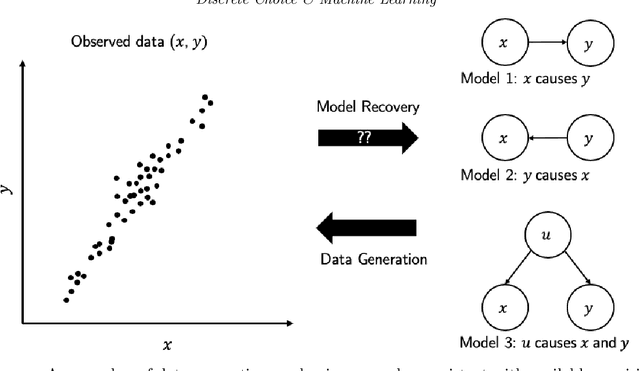
This paper introduces a new data-driven methodology for nested logit structure discovery. Nested logit models allow the modeling of positive correlations between the error terms of the utility specifications of the different alternatives in a discrete choice scenario through the specification of a nesting structure. Current nested logit model estimation practices require an a priori specification of a nesting structure by the modeler. In this we work we optimize over all possible specifications of the nested logit model that are consistent with rational utility maximization. We formulate the problem of learning an optimal nesting structure from the data as a mixed integer nonlinear programming (MINLP) optimization problem and solve it using a variant of the linear outer approximation algorithm. We exploit the tree structure of the problem and utilize the latest advances in integer optimization to bring practical tractability to the optimization problem we introduce. We demonstrate the ability of our algorithm to correctly recover the true nesting structure from synthetic data in a Monte Carlo experiment. In an empirical illustration using a stated preference survey on modes of transportation in the U.S. state of Massachusetts, we use our algorithm to obtain an optimal nesting tree representing the correlations between the unobserved effects of the different travel mode choices. We provide our implementation as a customizable and open-source code base written in the Julia programming language.

A Neural-embedded Choice Model: TasteNet-MNL Modeling Taste Heterogeneity with Flexibility and Interpretability

Discrete choice models (DCMs) and neural networks (NNs) can complement each other. We propose a neural network embedded choice model - TasteNet-MNL, to improve the flexibility in modeling taste heterogeneity while keeping model interpretability. The hybrid model consists of a TasteNet module: a feed-forward neural network that learns taste parameters as flexible functions of individual characteristics; and a choice module: a multinomial logit model (MNL) with manually specified utility. TasteNet and MNL are fully integrated and jointly estimated. By embedding a neural network into a DCM, we exploit a neural network's function approximation capacity to reduce specification bias. Through special structure and parameter constraints, we incorporate expert knowledge to regularize the neural network and maintain interpretability. On synthetic data, we show that TasteNet-MNL can recover the underlying non-linear utility function, and provide predictions and interpretations as accurate as the true model; while examples of logit or random coefficient logit models with misspecified utility functions result in large parameter bias and low predictability. In the case study of Swissmetro mode choice, TasteNet-MNL outperforms benchmarking MNLs' predictability; and discovers a wider spectrum of taste variations within the population, and higher values of time on average. This study takes an initial step towards developing a framework to combine theory-based and data-driven approaches for discrete choice modeling.

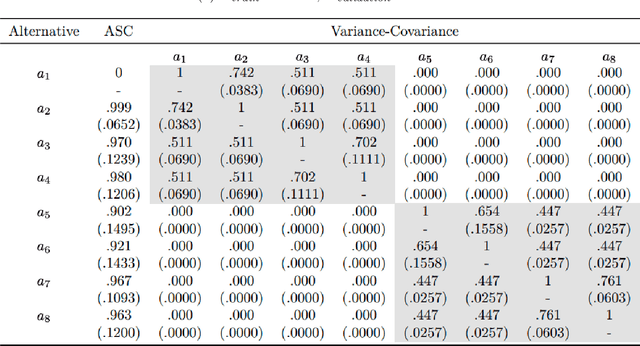
Sparse Covariance Estimation in Logit Mixture Models

This paper introduces a new data-driven methodology for estimating sparse covariance matrices of the random coefficients in logit mixture models. Researchers typically specify covariance matrices in logit mixture models under one of two extreme assumptions: either an unrestricted full covariance matrix (allowing correlations between all random coefficients), or a restricted diagonal matrix (allowing no correlations at all). Our objective is to find optimal subsets of correlated coefficients for which we estimate covariances. We propose a new estimator, called MISC, that uses a mixed-integer optimization (MIO) program to find an optimal block diagonal structure specification for the covariance matrix, corresponding to subsets of correlated coefficients, for any desired sparsity level using Markov Chain Monte Carlo (MCMC) posterior draws from the unrestricted full covariance matrix. The optimal sparsity level of the covariance matrix is determined using out-of-sample validation. We demonstrate the ability of MISC to correctly recover the true covariance structure from synthetic data. In an empirical illustration using a stated preference survey on modes of transportation, we use MISC to obtain a sparse covariance matrix indicating how preferences for attributes are related to one another.