Learning Structure in Nested Logit Models
Paper and Code
Aug 18, 2020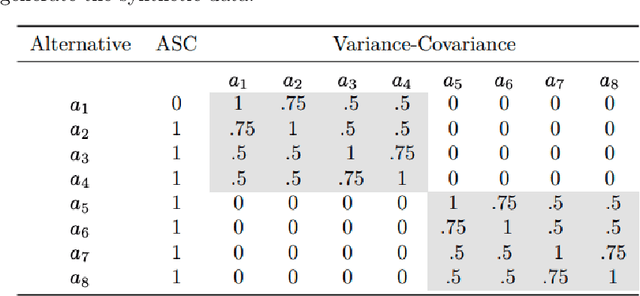
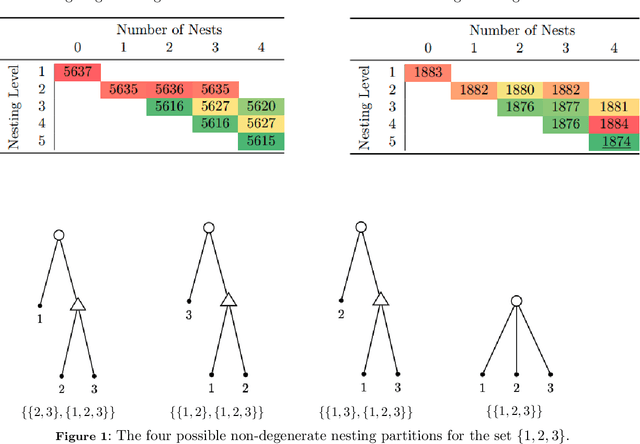
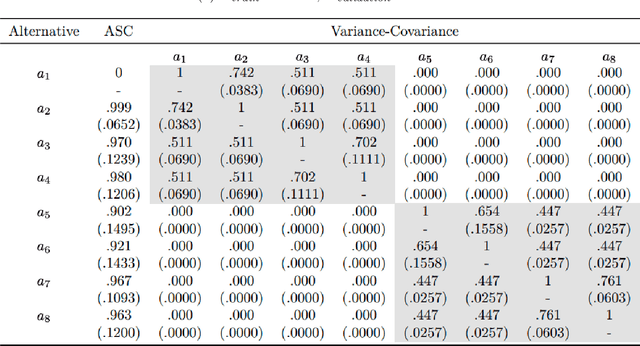
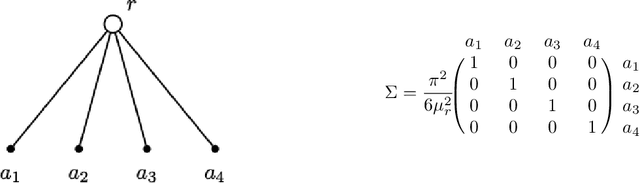
This paper introduces a new data-driven methodology for nested logit structure discovery. Nested logit models allow the modeling of positive correlations between the error terms of the utility specifications of the different alternatives in a discrete choice scenario through the specification of a nesting structure. Current nested logit model estimation practices require an a priori specification of a nesting structure by the modeler. In this we work we optimize over all possible specifications of the nested logit model that are consistent with rational utility maximization. We formulate the problem of learning an optimal nesting structure from the data as a mixed integer nonlinear programming (MINLP) optimization problem and solve it using a variant of the linear outer approximation algorithm. We exploit the tree structure of the problem and utilize the latest advances in integer optimization to bring practical tractability to the optimization problem we introduce. We demonstrate the ability of our algorithm to correctly recover the true nesting structure from synthetic data in a Monte Carlo experiment. In an empirical illustration using a stated preference survey on modes of transportation in the U.S. state of Massachusetts, we use our algorithm to obtain an optimal nesting tree representing the correlations between the unobserved effects of the different travel mode choices. We provide our implementation as a customizable and open-source code base written in the Julia programming language.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge