Latency Guarantee for Ubiquitous Intelligence in 6G: A Network Calculus Approach

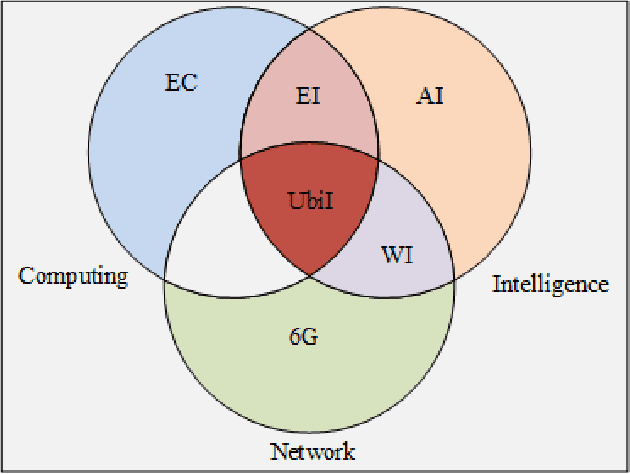
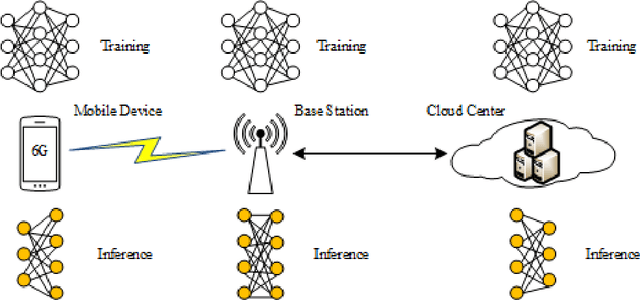
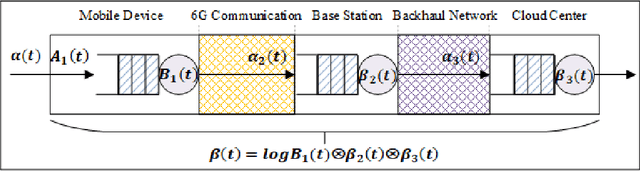
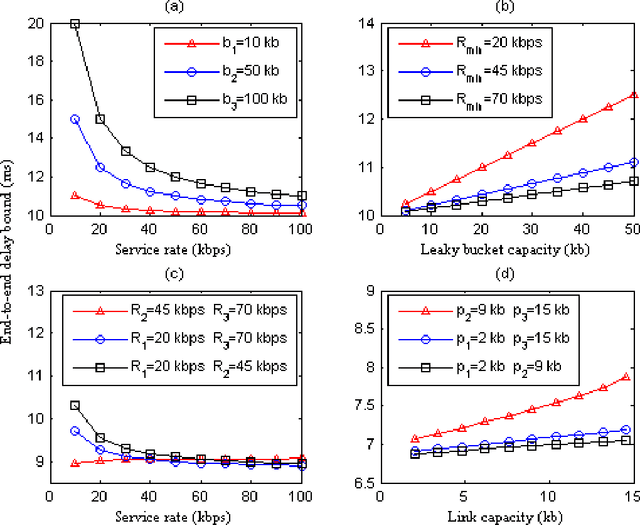
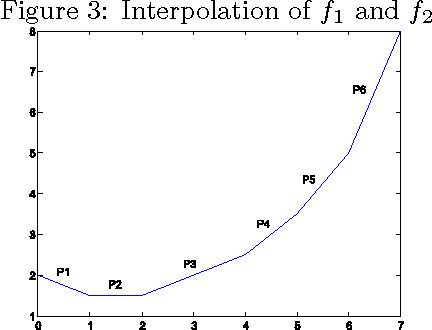
With the gradual deployment of 5G and the continuous popularization of edge intelligence (EI), the explosive growth of data on the edge of the network has promoted the rapid development of 6G and ubiquitous intelligence (UbiI). This article aims to explore a new method for modeling latency guarantees for UbiI in 6G given 6G's extremely stochastic nature in terahertz (THz) environments, THz channel tail behavior, and delay distribution tail characteristics generated by the UBiI random component, and to find the optimal solution that minimizes the end-to-end (E2E) delay of UbiI. In this article, the arrival curve and service curve of network calculus can well characterize the stochastic nature of wireless channels, the tail behavior of wireless systems and the E2E service curve of network calculus can model the tail characteristic of the delay distribution in UbiI. Specifically, we first propose demands and challenges facing 6G, edge computing (EC), edge deep learning (DL), and UbiI. Then, we propose the hierarchical architecture, the network model, and the service delay model of the UbiI system based on network calculus. In addition, two case studies demonstrate the usefulness and effectiveness of the network calculus approach in analyzing and modeling the latency guarantee for UbiI in 6G. Finally, future open research issues regarding the latency guarantee for UbiI in 6G are outlined.

Reinforcement Learning for Flexibility Design Problems

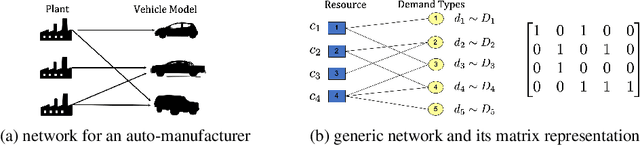
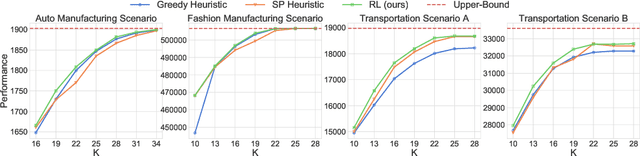
Flexibility design problems are a class of problems that appear in strategic decision-making across industries, where the objective is to design a ($e.g.$, manufacturing) network that affords flexibility and adaptivity. The underlying combinatorial nature and stochastic objectives make flexibility design problems challenging for standard optimization methods. In this paper, we develop a reinforcement learning (RL) framework for flexibility design problems. Specifically, we carefully design mechanisms with noisy exploration and variance reduction to ensure empirical success and show the unique advantage of RL in terms of fast-adaptation. Empirical results show that the RL-based method consistently finds better solutions compared to classical heuristics.

Belief Propagation for Min-cost Network Flow: Convergence and Correctness

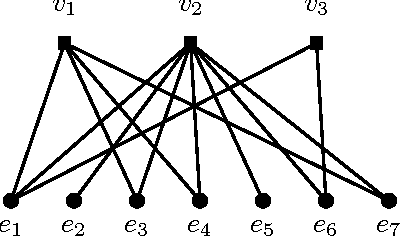
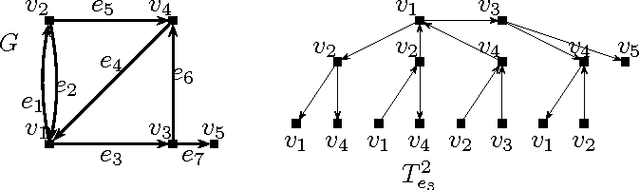
Message passing type algorithms such as the so-called Belief Propagation algorithm have recently gained a lot of attention in the statistics, signal processing and machine learning communities as attractive algorithms for solving a variety of optimization and inference problems. As a decentralized, easy to implement and empirically successful algorithm, BP deserves attention from the theoretical standpoint, and here not much is known at the present stage. In order to fill this gap we consider the performance of the BP algorithm in the context of the capacitated minimum-cost network flow problem - the classical problem in the operations research field. We prove that BP converges to the optimal solution in the pseudo-polynomial time, provided that the optimal solution of the underlying problem is unique and the problem input is integral. Moreover, we present a simple modification of the BP algorithm which gives a fully polynomial-time randomized approximation scheme (FPRAS) for the same problem, which no longer requires the uniqueness of the optimal solution. This is the first instance where BP is proved to have fully-polynomial running time. Our results thus provide a theoretical justification for the viability of BP as an attractive method to solve an important class of optimization problems.