DB3D-L: Depth-aware BEV Feature Transformation for Accurate 3D Lane Detection

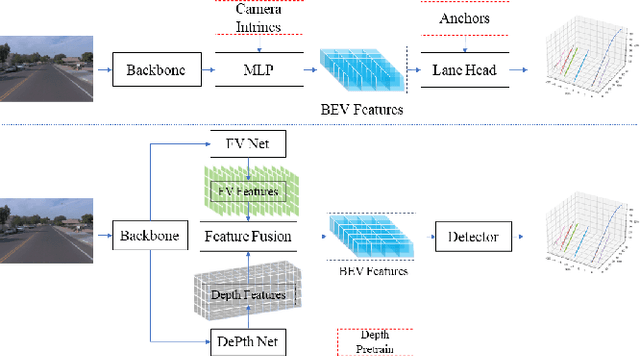
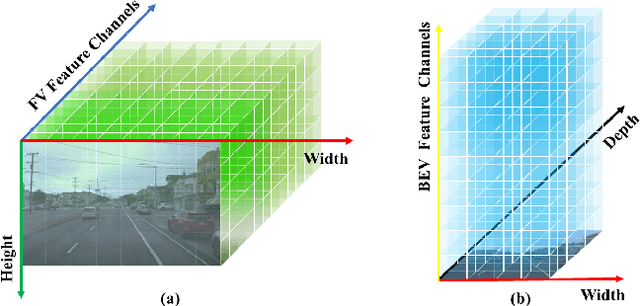
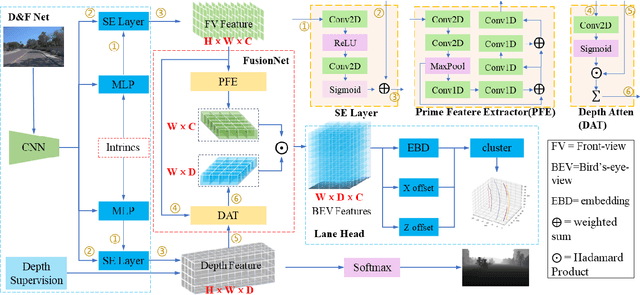
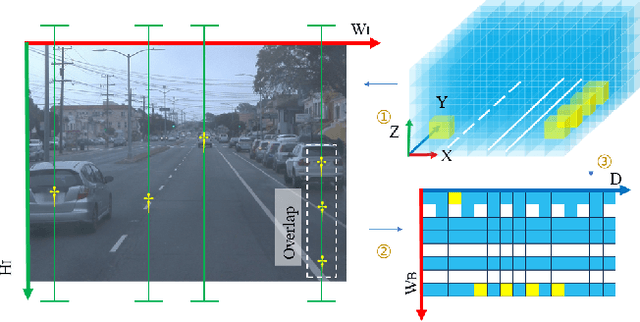
3D Lane detection plays an important role in autonomous driving. Recent advances primarily build Birds-Eye-View (BEV) feature from front-view (FV) images to perceive 3D information of Lane more effectively. However, constructing accurate BEV information from FV image is limited due to the lacking of depth information, causing previous works often rely heavily on the assumption of a flat ground plane. Leveraging monocular depth estimation to assist in constructing BEV features is less constrained, but existing methods struggle to effectively integrate the two tasks. To address the above issue, in this paper, an accurate 3D lane detection method based on depth-aware BEV feature transtormation is proposed. In detail, an effective feature extraction module is designed, in which a Depth Net is integrated to obtain the vital depth information for 3D perception, thereby simplifying the complexity of view transformation. Subquently a feature reduce module is proposed to reduce height dimension of FV features and depth features, thereby enables effective fusion of crucial FV features and depth features. Then a fusion module is designed to build BEV feature from prime FV feature and depth information. The proposed method performs comparably with state-of-the-art methods on both synthetic Apollo, realistic OpenLane datasets.

An Explicit Method for Fast Monocular Depth Recovery in Corridor Environments

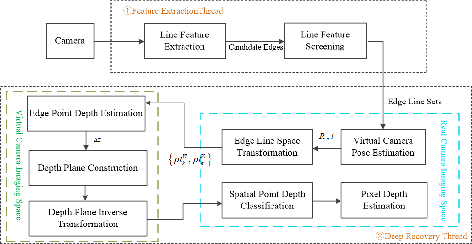
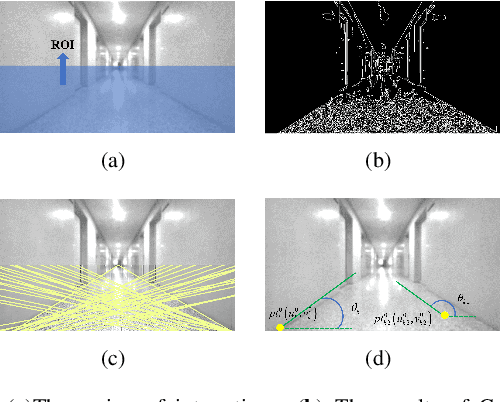
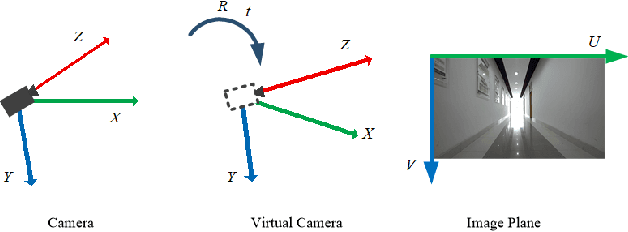
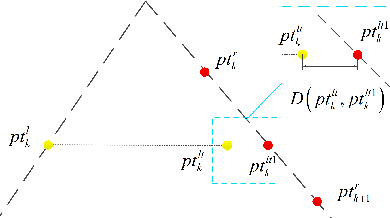
Monocular cameras are extensively employed in indoor robotics, but their performance is limited in visual odometry, depth estimation, and related applications due to the absence of scale information.Depth estimation refers to the process of estimating a dense depth map from the corresponding input image, existing researchers mostly address this issue through deep learning-based approaches, yet their inference speed is slow, leading to poor real-time capabilities. To tackle this challenge, we propose an explicit method for rapid monocular depth recovery specifically designed for corridor environments, leveraging the principles of nonlinear optimization. We adopt the virtual camera assumption to make full use of the prior geometric features of the scene. The depth estimation problem is transformed into an optimization problem by minimizing the geometric residual. Furthermore, a novel depth plane construction technique is introduced to categorize spatial points based on their possible depths, facilitating swift depth estimation in enclosed structural scenarios, such as corridors. We also propose a new corridor dataset, named Corr\_EH\_z, which contains images as captured by the UGV camera of a variety of corridors. An exhaustive set of experiments in different corridors reveal the efficacy of the proposed algorithm.

The Peril of Popular Deep Learning Uncertainty Estimation Methods

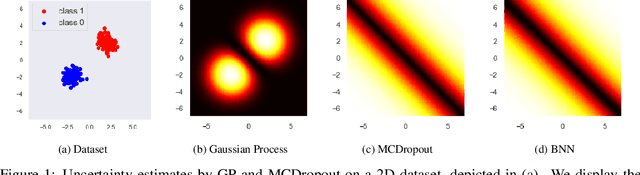
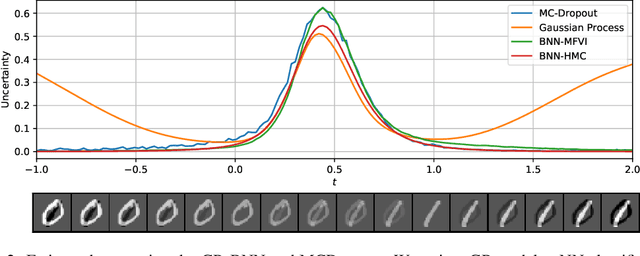
Uncertainty estimation (UE) techniques -- such as the Gaussian process (GP), Bayesian neural networks (BNN), Monte Carlo dropout (MCDropout) -- aim to improve the interpretability of machine learning models by assigning an estimated uncertainty value to each of their prediction outputs. However, since too high uncertainty estimates can have fatal consequences in practice, this paper analyzes the above techniques. Firstly, we show that GP methods always yield high uncertainty estimates on out of distribution (OOD) data. Secondly, we show on a 2D toy example that both BNNs and MCDropout do not give high uncertainty estimates on OOD samples. Finally, we show empirically that this pitfall of BNNs and MCDropout holds on real world datasets as well. Our insights (i) raise awareness for the more cautious use of currently popular UE methods in Deep Learning, (ii) encourage the development of UE methods that approximate GP-based methods -- instead of BNNs and MCDropout, and (iii) our empirical setups can be used for verifying the OOD performances of any other UE method. The source code is available at https://github.com/epfml/uncertainity-estimation.

Can we learn gradients by Hamiltonian Neural Networks?

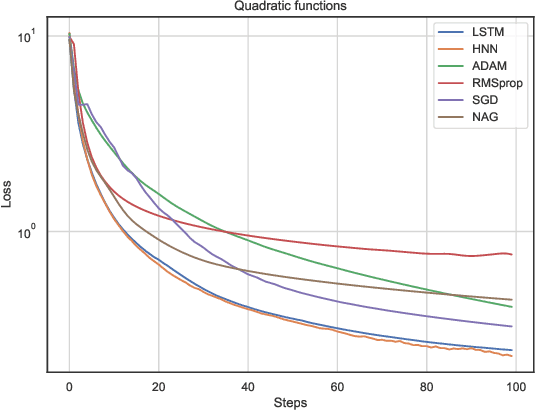
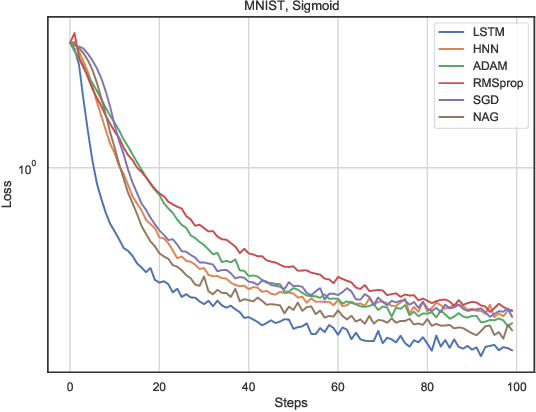
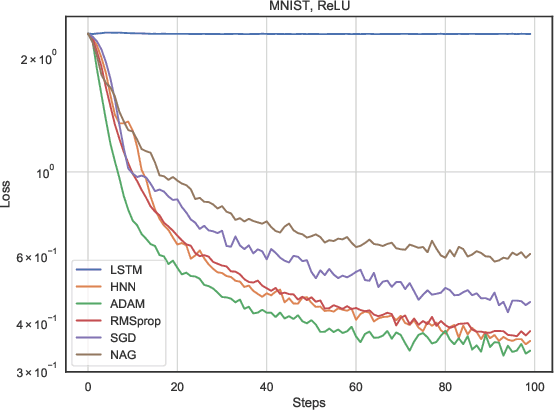
In this work, we propose a meta-learner based on ODE neural networks that learns gradients. This approach makes the optimizer is more flexible inducing an automatic inductive bias to the given task. Using the simplest Hamiltonian Neural Network we demonstrate that our method outperforms a meta-learner based on LSTM for an artificial task and the MNIST dataset with ReLU activations in the optimizee. Furthermore, it also surpasses the classic optimization methods for the artificial task and achieves comparable results for MNIST.