Deep Convolutional Architectures for Extrapolative Forecast in Time-dependent Flow Problems

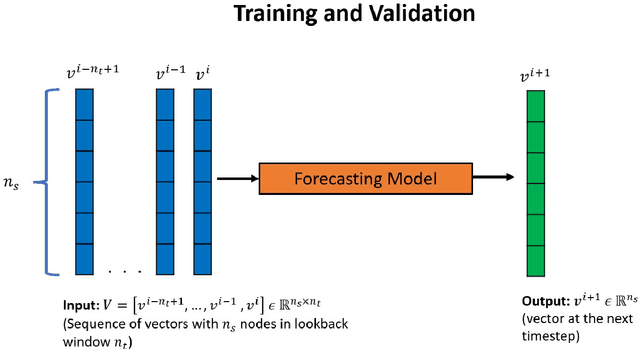
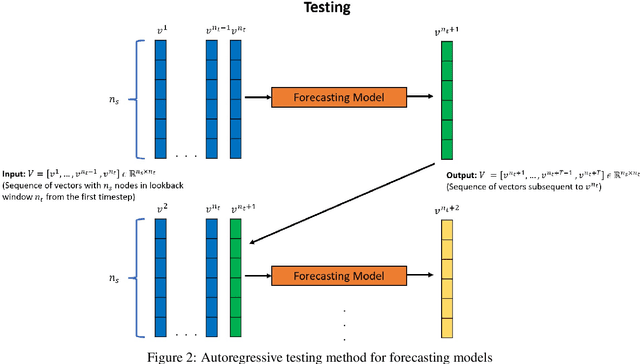
Physical systems whose dynamics are governed by partial differential equations (PDEs) find applications in numerous fields, from engineering design to weather forecasting. The process of obtaining the solution from such PDEs may be computationally expensive for large-scale and parameterized problems. In this work, deep learning techniques developed especially for time-series forecasts, such as LSTM and TCN, or for spatial-feature extraction such as CNN, are employed to model the system dynamics for advection dominated problems. These models take as input a sequence of high-fidelity vector solutions for consecutive time-steps obtained from the PDEs and forecast the solutions for the subsequent time-steps using auto-regression; thereby reducing the computation time and power needed to obtain such high-fidelity solutions. The models are tested on numerical benchmarks (1D Burgers' equation and Stoker's dam break problem) to assess the long-term prediction accuracy, even outside the training domain (extrapolation). Non-intrusive reduced-order modelling techniques such as deep auto-encoder networks are utilized to compress the high-fidelity snapshots before feeding them as input to the forecasting models in order to reduce the complexity and the required computations in the online and offline stages. Deep ensembles are employed to perform uncertainty quantification of the forecasting models, which provides information about the variance of the predictions as a result of the epistemic uncertainties.

Energy networks for state estimation with random sensors using sparse labels

State estimation is required whenever we deal with high-dimensional dynamical systems, as the complete measurement is often unavailable. It is key to gaining insight, performing control or optimizing design tasks. Most deep learning-based approaches require high-resolution labels and work with fixed sensor locations, thus being restrictive in their scope. Also, doing Proper orthogonal decomposition (POD) on sparse data is nontrivial. To tackle these problems, we propose a technique with an implicit optimization layer and a physics-based loss function that can learn from sparse labels. It works by minimizing the energy of the neural network prediction, enabling it to work with a varying number of sensors at different locations. Based on this technique we present two models for discrete and continuous prediction in space. We demonstrate the performance using two high-dimensional fluid problems of Burgers' equation and Flow Past Cylinder for discrete model and using Allen Cahn equation and Convection-diffusion equations for continuous model. We show the models are also robust to noise in measurements.

ML-Based Analysis to Identify Speech Features Relevant in Predicting Alzheimer's Disease

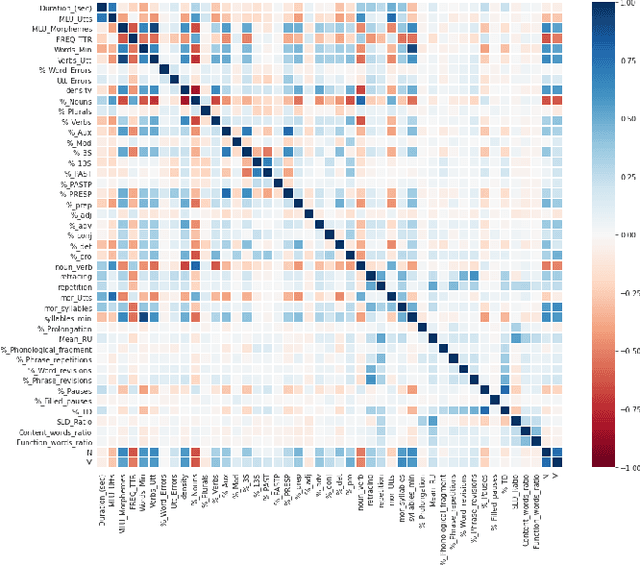
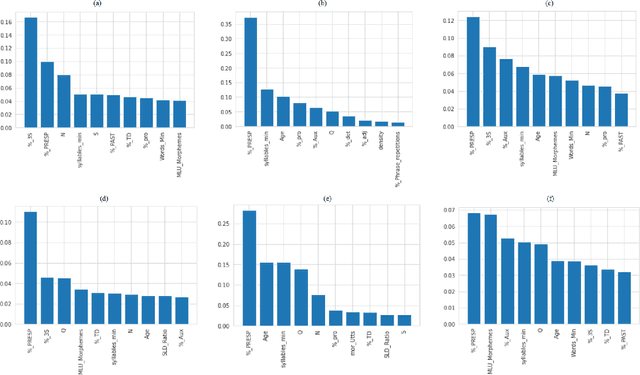
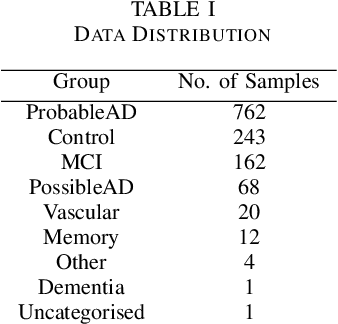
Alzheimer's disease (AD) is a neurodegenerative disease that affects nearly 50 million individuals across the globe and is one of the leading causes of deaths globally. It is projected that by 2050, the number of people affected by the disease would more than double. Consequently, the growing advancements in technology beg the question, can technology be used to predict Alzheimer's for a better and early diagnosis? In this paper, we focus on this very problem. Specifically, we have trained both ML models and neural networks to predict and classify participants based on their speech patterns. We computed a number of linguistic variables using DementiaBank's Pitt Corpus, a database consisting of transcripts of interviews with subjects suffering from multiple neurodegenerative diseases. We then trained both binary classifiers, as well as multiclass classifiers to distinguish AD from normal aging and other neurodegenerative diseases. We also worked on establishing the link between specific speech factors that can help determine the onset of AD. Confusion matrices and feature importance graphs have been plotted model-wise to compare the performances of our models. In both multiclass and binary classification, neural networks were found to outperform the other models with a testing accuracy of 76.44% and 92.05% respectively. For the feature importance, it was concluded that '%_PRESP' (present participle), '%_3S' (3rd person present tense markers) were two of the most important speech features for our classifiers in predicting AD.

GrADE: A graph based data-driven solver for time-dependent nonlinear partial differential equations

The physical world is governed by the laws of physics, often represented in form of nonlinear partial differential equations (PDEs). Unfortunately, solution of PDEs is non-trivial and often involves significant computational time. With recent developments in the field of artificial intelligence and machine learning, the solution of PDEs using neural network has emerged as a domain with huge potential. However, most of the developments in this field are based on either fully connected neural networks (FNN) or convolutional neural networks (CNN). While FNN is computationally inefficient as the number of network parameters can be potentially huge, CNN necessitates regular grid and simpler domain. In this work, we propose a novel framework referred to as the Graph Attention Differential Equation (GrADE) for solving time dependent nonlinear PDEs. The proposed approach couples FNN, graph neural network, and recently developed Neural ODE framework. The primary idea is to use graph neural network for modeling the spatial domain, and Neural ODE for modeling the temporal domain. The attention mechanism identifies important inputs/features and assign more weightage to the same; this enhances the performance of the proposed framework. Neural ODE, on the other hand, results in constant memory cost and allows trading of numerical precision for speed. We also propose depth refinement as an effective technique for training the proposed architecture in lesser time with better accuracy. The effectiveness of the proposed framework is illustrated using 1D and 2D Burgers' equations. Results obtained illustrate the capability of the proposed framework in modeling PDE and its scalability to larger domains without the need for retraining.

State estimation with limited sensors -- A deep learning based approach

The importance of state estimation in fluid mechanics is well-established; it is required for accomplishing several tasks including design/optimization, active control, and future state prediction. A common tactic in this regards is to rely on reduced order models. Such approaches, in general, use measurement data of one-time instance. However, oftentimes data available from sensors is sequential and ignoring it results in information loss. In this paper, we propose a novel deep learning based state estimation framework that learns from sequential data. The proposed model structure consists of the recurrent cell to pass information from different time steps enabling utilization of this information to recover the full state. We illustrate that utilizing sequential data allows for state recovery from only one or two sensors. For efficient recovery of the state, the proposed approached is coupled with an auto-encoder based reduced order model. We illustrate the performance of the proposed approach using two examples and it is found to outperform other alternatives existing in the literature.