Differentiable Information Bottleneck for Deterministic Multi-view Clustering

In recent several years, the information bottleneck (IB) principle provides an information-theoretic framework for deep multi-view clustering (MVC) by compressing multi-view observations while preserving the relevant information of multiple views. Although existing IB-based deep MVC methods have achieved huge success, they rely on variational approximation and distribution assumption to estimate the lower bound of mutual information, which is a notoriously hard and impractical problem in high-dimensional multi-view spaces. In this work, we propose a new differentiable information bottleneck (DIB) method, which provides a deterministic and analytical MVC solution by fitting the mutual information without the necessity of variational approximation. Specifically, we first propose to directly fit the mutual information of high-dimensional spaces by leveraging normalized kernel Gram matrix, which does not require any auxiliary neural estimator to estimate the lower bound of mutual information. Then, based on the new mutual information measurement, a deterministic multi-view neural network with analytical gradients is explicitly trained to parameterize IB principle, which derives a deterministic compression of input variables from different views. Finally, a triplet consistency discovery mechanism is devised, which is capable of mining the feature consistency, cluster consistency and joint consistency based on the deterministic and compact representations. Extensive experimental results show the superiority of our DIB method on 6 benchmarks compared with 13 state-of-the-art baselines.

Representation Learning with Deconvolution for Multivariate Time Series Classification and Visualization

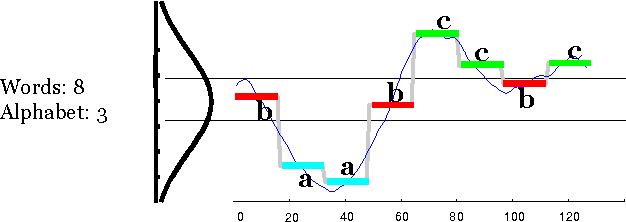
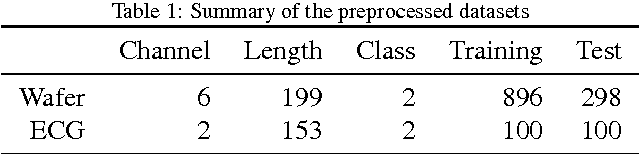
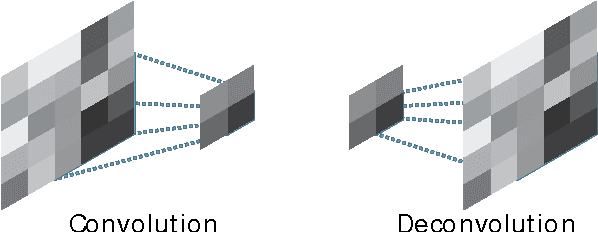
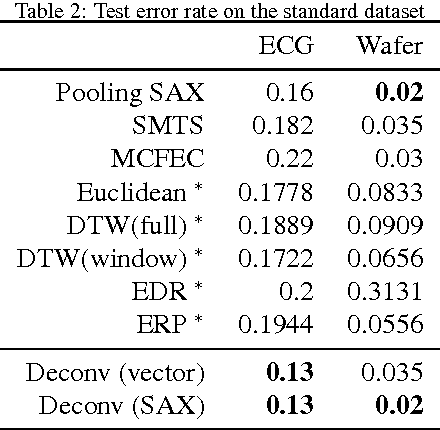
We propose a new model based on the deconvolutional networks and SAX discretization to learn the representation for multivariate time series. Deconvolutional networks fully exploit the advantage the powerful expressiveness of deep neural networks in the manner of unsupervised learning. We design a network structure specifically to capture the cross-channel correlation with deconvolution, forcing the pooling operation to perform the dimension reduction along each position in the individual channel. Discretization based on Symbolic Aggregate Approximation is applied on the feature vectors to further extract the bag of features. We show how this representation and bag of features helps on classification. A full comparison with the sequence distance based approach is provided to demonstrate the effectiveness of our approach on the standard datasets. We further build the Markov matrix from the discretized representation from the deconvolution to visualize the time series as complex networks, which show more class-specific statistical properties and clear structures with respect to different labels.

Empirical Studies on Symbolic Aggregation Approximation Under Statistical Perspectives for Knowledge Discovery in Time Series

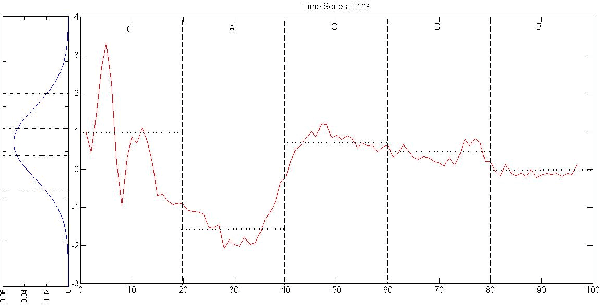
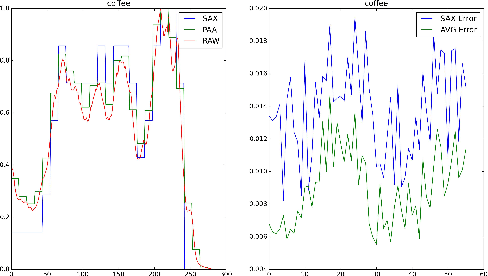
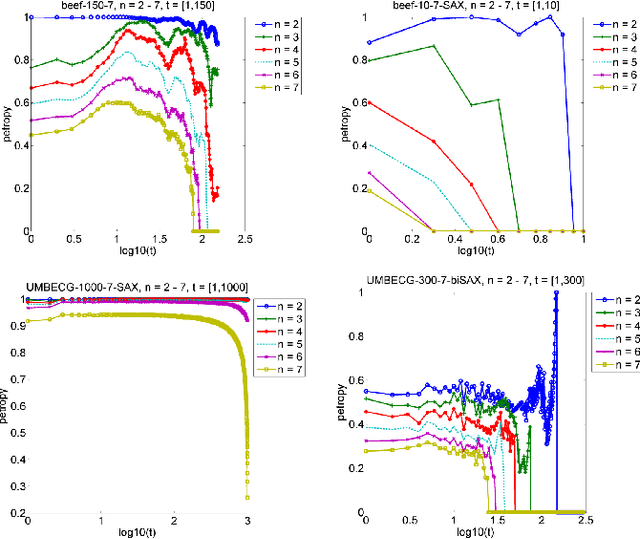
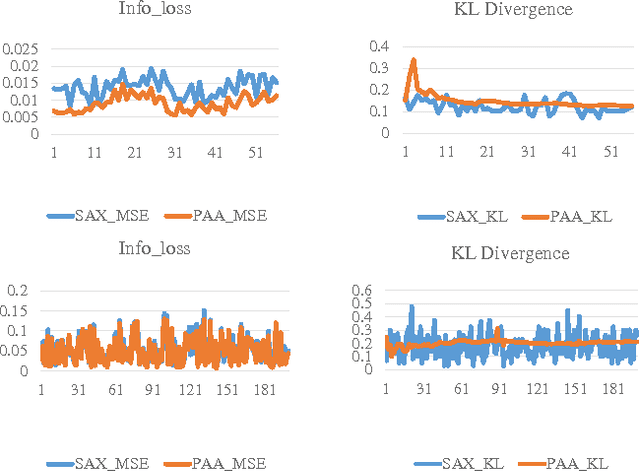
Symbolic Aggregation approXimation (SAX) has been the de facto standard representation methods for knowledge discovery in time series on a number of tasks and applications. So far, very little work has been done in empirically investigating the intrinsic properties and statistical mechanics in SAX words. In this paper, we applied several statistical measurements and proposed a new statistical measurement, i.e. information embedding cost (IEC) to analyze the statistical behaviors of the symbolic dynamics. Our experiments on the benchmark datasets and the clinical signals demonstrate that SAX can always reduce the complexity while preserving the core information embedded in the original time series with significant embedding efficiency. Our proposed IEC score provide a priori to determine if SAX is adequate for specific dataset, which can be generalized to evaluate other symbolic representations. Our work provides an analytical framework with several statistical tools to analyze, evaluate and further improve the symbolic dynamics for knowledge discovery in time series.