Distinct hydrologic response patterns and trends worldwide revealed by physics-embedded learning

To track rapid changes within our water sector, Global Water Models (GWMs) need to realistically represent hydrologic systems' response patterns - such as baseflow fraction - but are hindered by their limited ability to learn from data. Here we introduce a high-resolution physics-embedded big-data-trained model as a breakthrough in reliably capturing characteristic hydrologic response patterns ('signatures') and their shifts. By realistically representing the long-term water balance, the model revealed widespread shifts - up to ~20% over 20 years - in fundamental green-blue-water partitioning and baseflow ratios worldwide. Shifts in these response patterns, previously considered static, contributed to increasing flood risks in northern mid-latitudes, heightening water supply stresses in southern subtropical regions, and declining freshwater inputs to many European estuaries, all with ecological implications. With more accurate simulations at monthly and daily scales than current operational systems, this next-generation model resolves large, nonlinear seasonal runoff responses to rainfall ('elasticity') and streamflow flashiness in semi-arid and arid regions. These metrics highlight regions with management challenges due to large water supply variability and high climate sensitivity, but also provide tools to forecast seasonal water availability. This capability newly enables global-scale models to deliver reliable and locally relevant insights for water management.

Update hydrological states or meteorological forcings? Comparing data assimilation methods for differentiable hydrologic models

Data assimilation (DA) enables hydrologic models to update their internal states using near-real-time observations for more accurate forecasts. With deep neural networks like long short-term memory (LSTM), using either lagged observations as inputs (called "data integration") or variational DA has shown success in improving forecasts. However, it is unclear which methods are performant or optimal for physics-informed machine learning ("differentiable") models, which represent only a small amount of physically-meaningful states while using deep networks to supply parameters or missing processes. Here we developed variational DA methods for differentiable models, including optimizing adjusters for just precipitation data, just model internal hydrological states, or both. Our results demonstrated that differentiable streamflow models using the CAMELS dataset can benefit strongly and equivalently from variational DA as LSTM, with one-day lead time median Nash-Sutcliffe efficiency (NSE) elevated from 0.75 to 0.82. The resulting forecast matched or outperformed LSTM with DA in the eastern, northwestern, and central Great Plains regions of the conterminous United States. Both precipitation and state adjusters were needed to achieve these results, with the latter being substantially more effective on its own, and the former adding moderate benefits for high flows. Our DA framework does not need systematic training data and could serve as a practical DA scheme for whole river networks.

Scientific Machine Learning of Flow Resistance Using Universal Shallow Water Equations with Differentiable Programming

Shallow water equations (SWEs) are the backbone of most hydrodynamics models for flood prediction, river engineering, and many other water resources applications. The estimation of flow resistance, i.e., the Manning's roughness coefficient $n$, is crucial for ensuring model accuracy, and has been previously determined using empirical formulas or tables. To better account for temporal and spatial variability in channel roughness, inverse modeling of $n$ using observed flow data is more reliable and adaptable; however, it is challenging when using traditional SWE solvers. Based on the concept of universal differential equation (UDE), which combines physics-based differential equations with neural networks (NNs), we developed a universal SWEs (USWEs) solver, Hydrograd, for hybrid hydrodynamics modeling. It can do accurate forward simulations, support automatic differentiation (AD) for gradient-based sensitivity analysis and parameter inversion, and perform scientific machine learning for physics discovery. In this work, we first validated the accuracy of its forward modeling, then applied a real-world case to demonstrate the ability of USWEs to capture model sensitivity (gradients) and perform inverse modeling of Manning's $n$. Furthermore, we used a NN to learn a universal relationship between $n$, hydraulic parameters, and flow in a real river channel. Unlike inverse modeling using surrogate models, Hydrograd uses a two-dimensional SWEs solver as its physics backbone, which eliminates the need for data-intensive pretraining and resolves the generalization problem when applied to out-of-sample scenarios. This differentiable modeling approach, with seamless integration with NNs, provides a new pathway for solving complex inverse problems and discovering new physics in hydrodynamics.

Bathymetry Inversion using a Deep-Learning-Based Surrogate for Shallow Water Equations Solvers

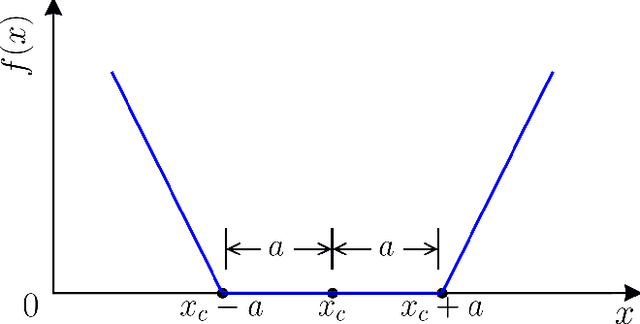
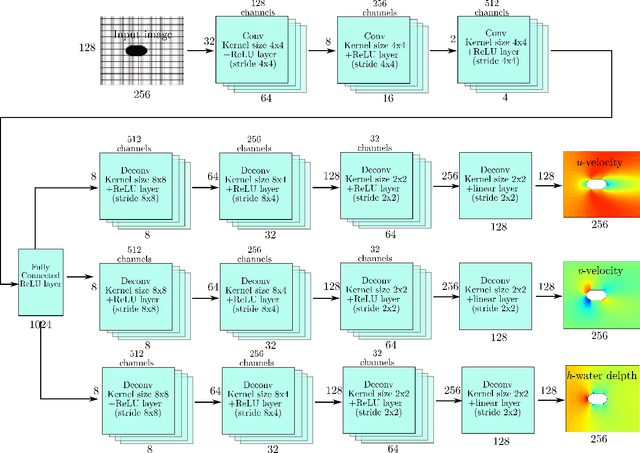
River bathymetry is critical for many aspects of water resources management. We propose and demonstrate a bathymetry inversion method using a deep-learning-based surrogate for shallow water equations solvers. The surrogate uses the convolutional autoencoder with a shared-encoder, separate-decoder architecture. It encodes the input bathymetry and decodes to separate outputs for flow-field variables. A gradient-based optimizer is used to perform bathymetry inversion with the trained surrogate. Two physically-based constraints on both bed elevation value and slope have to be added as inversion loss regularizations to obtain usable inversion results. Using the "L-curve" criterion, a heuristic approach was proposed to determine the regularization parameters. Both the surrogate model and the inversion algorithm show good performance. We found the bathymetry inversion process has two distinctive stages, which resembles the sculptural process of initial broad-brush calving and final detailing. The inversion loss due to flow prediction error reaches its minimum in the first stage and remains almost constant afterward. The bed elevation value and slope regularizations play the dominant role in the second stage in selecting the most probable solution. We also found the surrogate architecture (whether with both velocity and water surface elevation or velocity only as outputs) does not show significant impact on inversion result.

Surrogate Model for Shallow Water Equations Solvers with Deep Learning

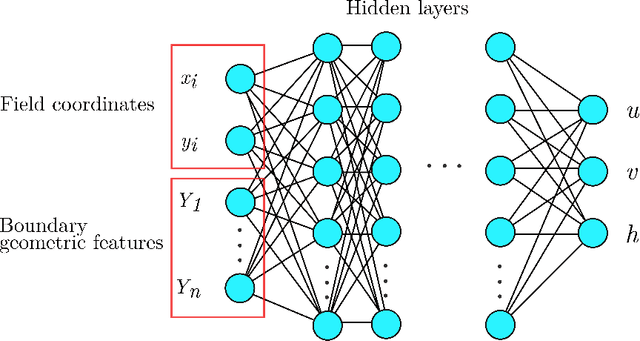
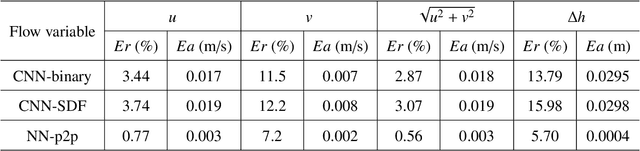
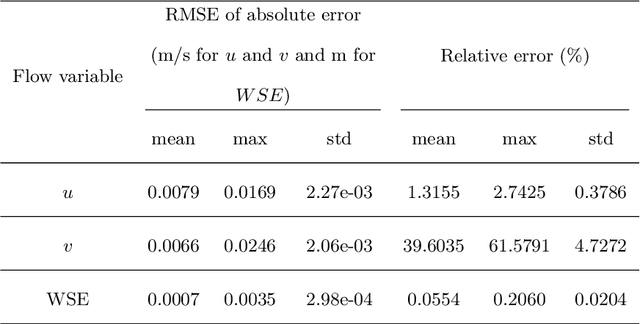
Shallow water equations are the foundation of most models for flooding and river hydraulics analysis. These physics-based models are usually expensive and slow to run, thus not suitable for real-time prediction or parameter inversion. An attractive alternative is surrogate model. This work introduces an efficient, accurate, and flexible surrogate model, NN-p2p, based on deep learning and it can make point-to-point predictions on unstructured or irregular meshes. The new method was evaluated and compared against existing methods based on convolutional neural networks (CNNs), which can only make image-to-image predictions on structured or regular meshes. In NN-p2p, the input includes both spatial coordinates and boundary features that can describe the geometry of hydraulic structures, such as bridge piers. All surrogate models perform well in predicting flow around different types of piers in the training domain. However, only NN-p2p works well when spatial extrapolation is performed. The limitations of CNN-based methods are rooted in their raster-image nature which cannot capture boundary geometry and flow features exactly, which are of paramount importance to fluid dynamics. NN-p2p also has good performance in predicting flow around piers unseen by the neural network. The NN-p2p model also respects conservation laws more strictly. The application of the proposed surrogate model was demonstrated by calculating the drag coefficient $C_D$ for piers and a new linear relationship between $C_D$ and the logarithmic transformation of pier's length/width ratio was discovered.