FDC-Net: Rethinking the association between EEG artifact removal and multi-dimensional affective computing

Electroencephalogram (EEG)-based emotion recognition holds significant value in affective computing and brain-computer interfaces. However, in practical applications, EEG recordings are susceptible to the effects of various physiological artifacts. Current approaches typically treat denoising and emotion recognition as independent tasks using cascaded architectures, which not only leads to error accumulation, but also fails to exploit potential synergies between these tasks. Moreover, conventional EEG-based emotion recognition models often rely on the idealized assumption of "perfectly denoised data", lacking a systematic design for noise robustness. To address these challenges, a novel framework that deeply couples denoising and emotion recognition tasks is proposed for end-to-end noise-robust emotion recognition, termed as Feedback-Driven Collaborative Network for Denoising-Classification Nexus (FDC-Net). Our primary innovation lies in establishing a dynamic collaborative mechanism between artifact removal and emotion recognition through: (1) bidirectional gradient propagation with joint optimization strategies; (2) a gated attention mechanism integrated with frequency-adaptive Transformer using learnable band-position encoding. Two most popular EEG-based emotion datasets (DEAP and DREAMER) with multi-dimensional emotional labels were employed to compare the artifact removal and emotion recognition performance between ASLSL and nine state-of-the-art methods. In terms of the denoising task, FDC-Net obtains a maximum correlation coefficient (CC) value of 96.30% on DEAP and a maximum CC value of 90.31% on DREAMER. In terms of the emotion recognition task under physiological artifact interference, FDC-Net achieves emotion recognition accuracies of 82.3+7.1% on DEAP and 88.1+0.8% on DREAMER.

CWEFS: Brain volume conduction effects inspired channel-wise EEG feature selection for multi-dimensional emotion recognition

Due to the intracranial volume conduction effects, high-dimensional multi-channel electroencephalography (EEG) features often contain substantial redundant and irrelevant information. This issue not only hinders the extraction of discriminative emotional representations but also compromises the real-time performance. Feature selection has been established as an effective approach to address the challenges while enhancing the transparency and interpretability of emotion recognition models. However, existing EEG feature selection research overlooks the influence of latent EEG feature structures on emotional label correlations and assumes uniform importance across various channels, directly limiting the precise construction of EEG feature selection models for multi-dimensional affective computing. To address these limitations, a novel channel-wise EEG feature selection (CWEFS) method is proposed for multi-dimensional emotion recognition. Specifically, inspired by brain volume conduction effects, CWEFS integrates EEG emotional feature selection into a shared latent structure model designed to construct a consensus latent space across diverse EEG channels. To preserve the local geometric structure, this consensus space is further integrated with the latent semantic analysis of multi-dimensional emotional labels. Additionally, CWEFS incorporates adaptive channel-weight learning to automatically determine the significance of different EEG channels in the emotional feature selection task. The effectiveness of CWEFS was validated using three popular EEG datasets with multi-dimensional emotional labels. Comprehensive experimental results, compared against nineteen feature selection methods, demonstrate that the EEG feature subsets chosen by CWEFS achieve optimal emotion recognition performance across six evaluation metrics.

ADSEL: Adaptive dual self-expression learning for EEG feature selection via incomplete multi-dimensional emotional tagging

EEG based multi-dimension emotion recognition has attracted substantial research interest in human computer interfaces. However, the high dimensionality of EEG features, coupled with limited sample sizes, frequently leads to classifier overfitting and high computational complexity. Feature selection constitutes a critical strategy for mitigating these challenges. Most existing EEG feature selection methods assume complete multi-dimensional emotion labels. In practice, open acquisition environment, and the inherent subjectivity of emotion perception often result in incomplete label data, which can compromise model generalization. Additionally, existing feature selection methods for handling incomplete multi-dimensional labels primarily focus on correlations among various dimensions during label recovery, neglecting the correlation between samples in the label space and their interaction with various dimensions. To address these issues, we propose a novel incomplete multi-dimensional feature selection algorithm for EEG-based emotion recognition. The proposed method integrates an adaptive dual self-expression learning (ADSEL) with least squares regression. ADSEL establishes a bidirectional pathway between sample-level and dimension-level self-expression learning processes within the label space. It could facilitate the cross-sharing of learned information between these processes, enabling the simultaneous exploitation of effective information across both samples and dimensions for label reconstruction. Consequently, ADSEL could enhances label recovery accuracy and effectively identifies the optimal EEG feature subset for multi-dimensional emotion recognition.

Embedded Multi-label Feature Selection via Orthogonal Regression

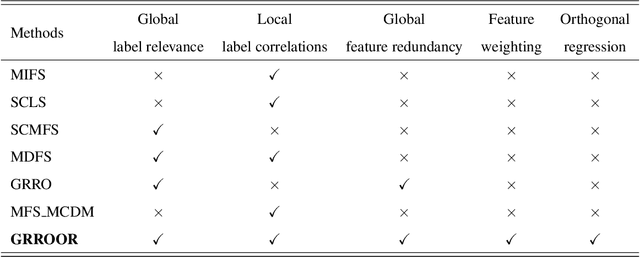
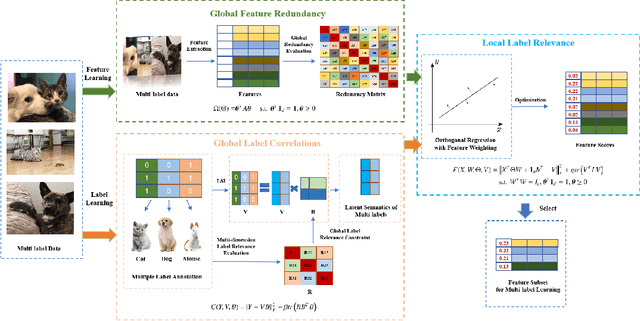
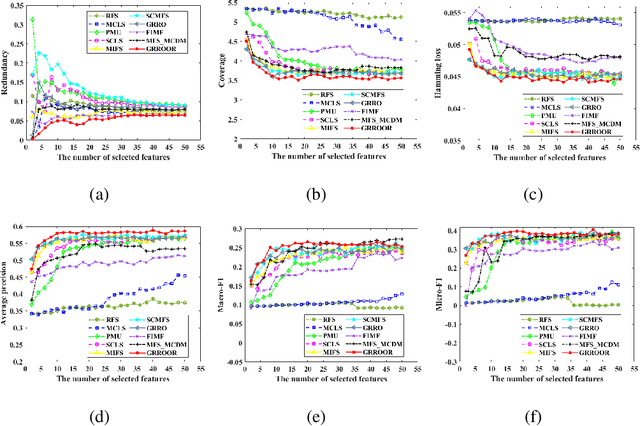
In the last decade, embedded multi-label feature selection methods, incorporating the search for feature subsets into model optimization, have attracted considerable attention in accurately evaluating the importance of features in multi-label classification tasks. Nevertheless, the state-of-the-art embedded multi-label feature selection algorithms based on least square regression usually cannot preserve sufficient discriminative information in multi-label data. To tackle the aforementioned challenge, a novel embedded multi-label feature selection method, termed global redundancy and relevance optimization in orthogonal regression (GRROOR), is proposed to facilitate the multi-label feature selection. The method employs orthogonal regression with feature weighting to retain sufficient statistical and structural information related to local label correlations of the multi-label data in the feature learning process. Additionally, both global feature redundancy and global label relevancy information have been considered in the orthogonal regression model, which could contribute to the search for discriminative and non-redundant feature subsets in the multi-label data. The cost function of GRROOR is an unbalanced orthogonal Procrustes problem on the Stiefel manifold. A simple yet effective scheme is utilized to obtain an optimal solution. Extensive experimental results on ten multi-label data sets demonstrate the effectiveness of GRROOR.

Supervised feature selection with orthogonal regression and feature weighting

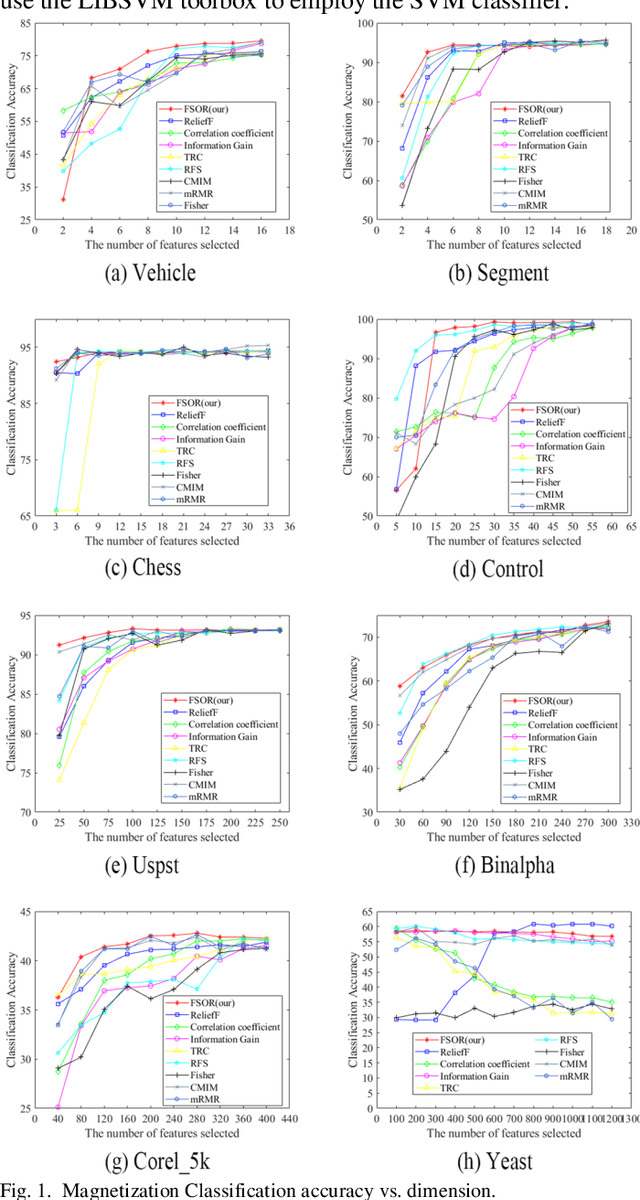
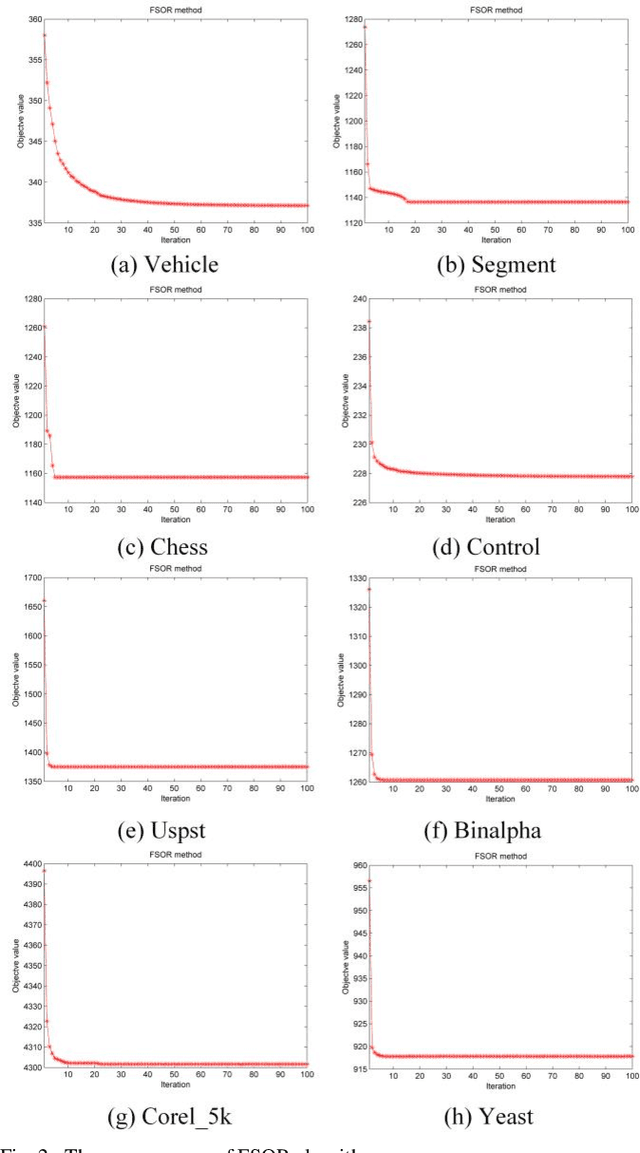
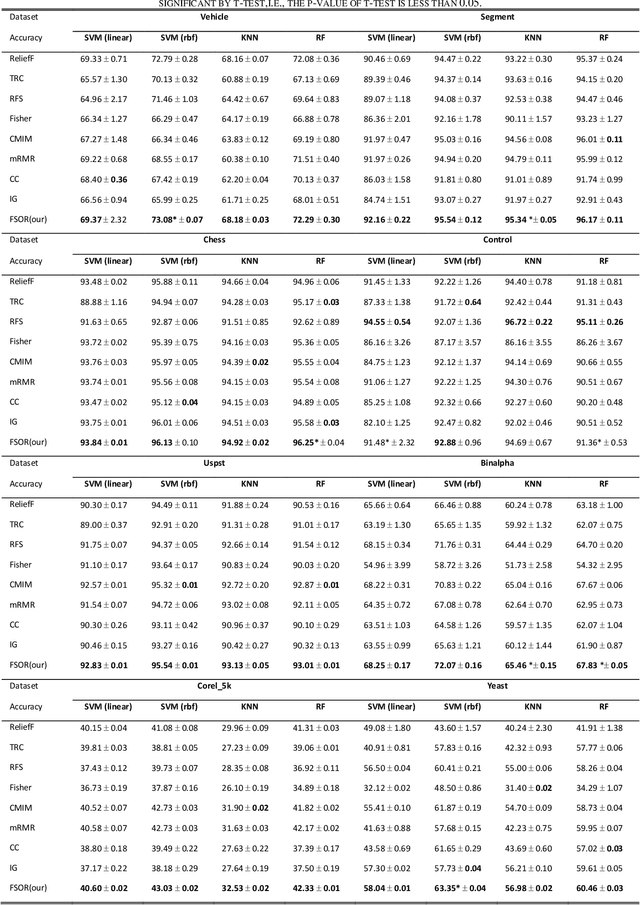
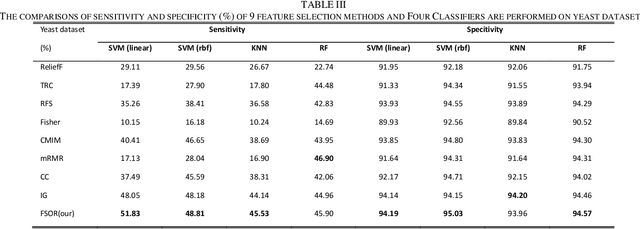
Effective features can improve the performance of a model, which can thus help us understand the characteristics and underlying structure of complex data. Previous feature selection methods usually cannot keep more local structure information. To address the defects previously mentioned, we propose a novel supervised orthogonal least square regression model with feature weighting for feature selection. The optimization problem of the objection function can be solved by employing generalized power iteration (GPI) and augmented Lagrangian multiplier (ALM) methods. Experimental results show that the proposed method can more effectively reduce the feature dimensionality and obtain better classification results than traditional feature selection methods. The convergence of our iterative method is proved as well. Consequently, the effectiveness and superiority of the proposed method are verified both theoretically and experimentally.