Supervised feature selection with orthogonal regression and feature weighting
Paper and Code
Oct 09, 2019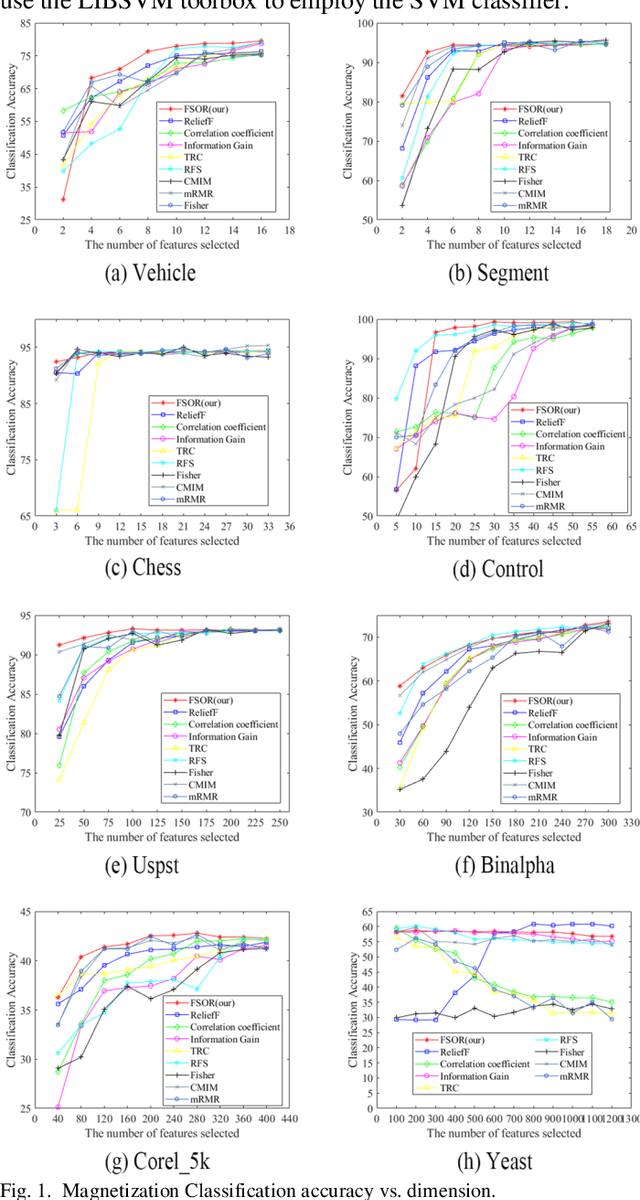
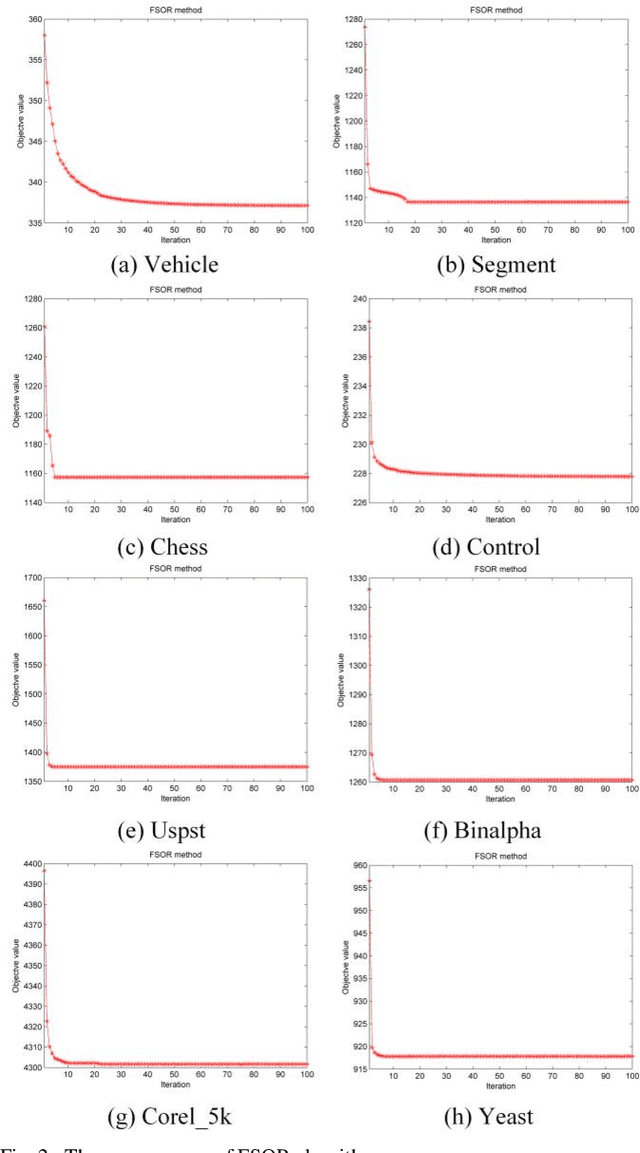
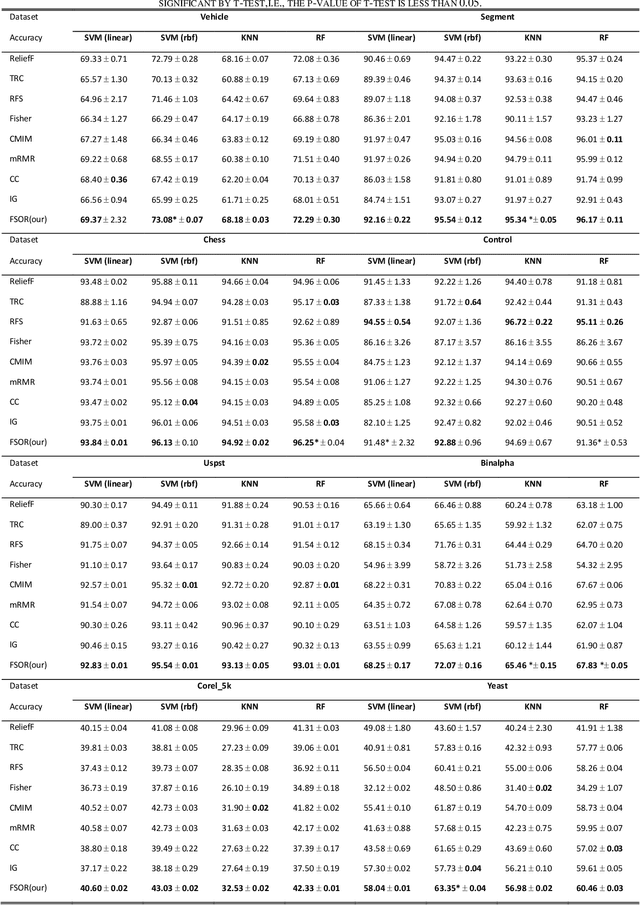
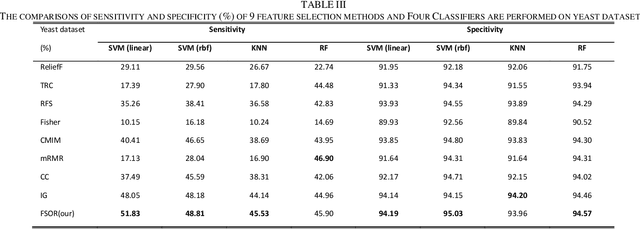
Effective features can improve the performance of a model, which can thus help us understand the characteristics and underlying structure of complex data. Previous feature selection methods usually cannot keep more local structure information. To address the defects previously mentioned, we propose a novel supervised orthogonal least square regression model with feature weighting for feature selection. The optimization problem of the objection function can be solved by employing generalized power iteration (GPI) and augmented Lagrangian multiplier (ALM) methods. Experimental results show that the proposed method can more effectively reduce the feature dimensionality and obtain better classification results than traditional feature selection methods. The convergence of our iterative method is proved as well. Consequently, the effectiveness and superiority of the proposed method are verified both theoretically and experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge