Phase-space entropy at acquisition reflects downstream learnability

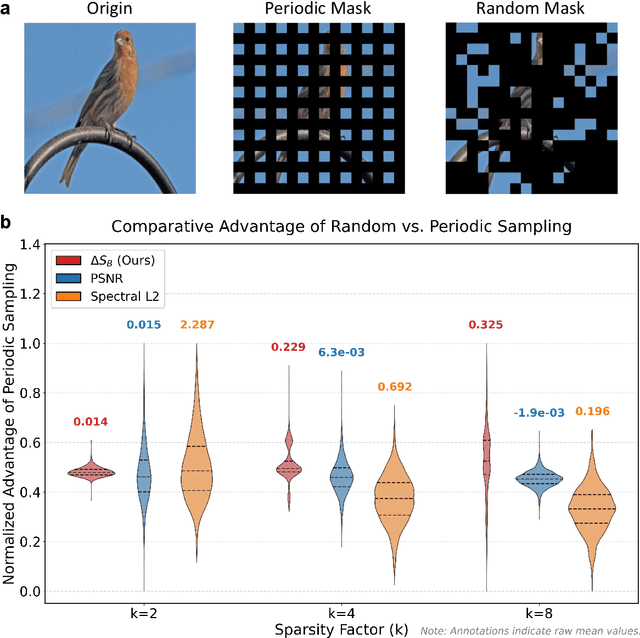
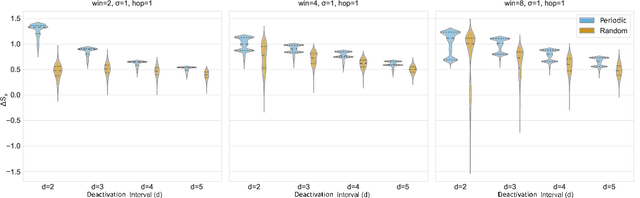
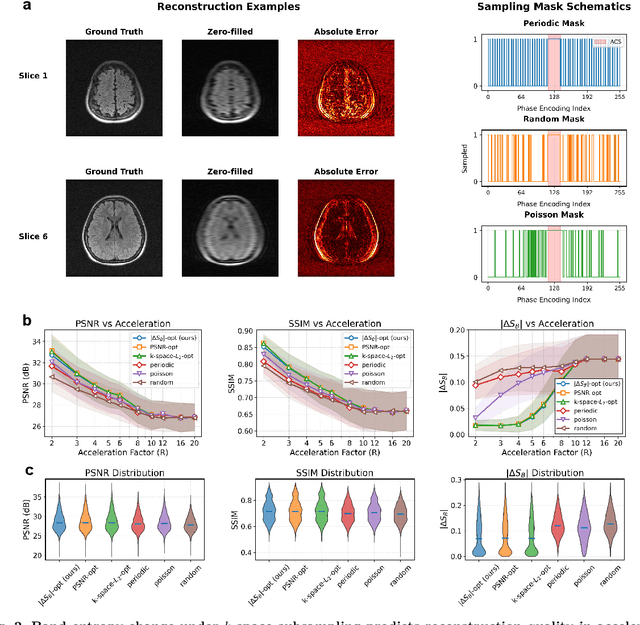
Modern learning systems work with data that vary widely across domains, but they all ultimately depend on how much structure is already present in the measurements before any model is trained. This raises a basic question: is there a general, modality-agnostic way to quantify how acquisition itself preserves or destroys the information that downstream learners could use? Here we propose an acquisition-level scalar $ΔS_{\mathcal B}$ based on instrument-resolved phase space. Unlike pixelwise distortion or purely spectral errors that often saturate under aggressive undersampling, $ΔS_{\mathcal B}$ directly quantifies how acquisition mixes or removes joint space--frequency structure at the instrument scale. We show theoretically that \(ΔS_{\mathcal B}\) correctly identifies the phase-space coherence of periodic sampling as the physical source of aliasing, recovering classical sampling-theorem consequences. Empirically, across masked image classification, accelerated MRI, and massive MIMO (including over-the-air measurements), $|ΔS_{\mathcal B}|$ consistently ranks sampling geometries and predicts downstream reconstruction/recognition difficulty \emph{without training}. In particular, minimizing $|ΔS_{\mathcal B}|$ enables zero-training selection of variable-density MRI mask parameters that matches designs tuned by conventional pre-reconstruction criteria. These results suggest that phase-space entropy at acquisition reflects downstream learnability, enabling pre-training selection of candidate sampling policies and as a shared notion of information preservation across modalities.

Is AI Robust Enough for Scientific Research?

We uncover a phenomenon largely overlooked by the scientific community utilizing AI: neural networks exhibit high susceptibility to minute perturbations, resulting in significant deviations in their outputs. Through an analysis of five diverse application areas -- weather forecasting, chemical energy and force calculations, fluid dynamics, quantum chromodynamics, and wireless communication -- we demonstrate that this vulnerability is a broad and general characteristic of AI systems. This revelation exposes a hidden risk in relying on neural networks for essential scientific computations, calling further studies on their reliability and security.

Symmetry Breaking in Neural Network Optimization: Insights from Input Dimension Expansion

Understanding the mechanisms behind neural network optimization is crucial for improving network design and performance. While various optimization techniques have been developed, a comprehensive understanding of the underlying principles that govern these techniques remains elusive. Specifically, the role of symmetry breaking, a fundamental concept in physics, has not been fully explored in neural network optimization. This gap in knowledge limits our ability to design networks that are both efficient and effective. Here, we propose the symmetry breaking hypothesis to elucidate the significance of symmetry breaking in enhancing neural network optimization. We demonstrate that a simple input expansion can significantly improve network performance across various tasks, and we show that this improvement can be attributed to the underlying symmetry breaking mechanism. We further develop a metric to quantify the degree of symmetry breaking in neural networks, providing a practical approach to evaluate and guide network design. Our findings confirm that symmetry breaking is a fundamental principle that underpins various optimization techniques, including dropout, batch normalization, and equivariance. By quantifying the degree of symmetry breaking, our work offers a practical technique for performance enhancement and a metric to guide network design without the need for complete datasets and extensive training processes.