Symmetry Breaking in Neural Network Optimization: Insights from Input Dimension Expansion

Understanding the mechanisms behind neural network optimization is crucial for improving network design and performance. While various optimization techniques have been developed, a comprehensive understanding of the underlying principles that govern these techniques remains elusive. Specifically, the role of symmetry breaking, a fundamental concept in physics, has not been fully explored in neural network optimization. This gap in knowledge limits our ability to design networks that are both efficient and effective. Here, we propose the symmetry breaking hypothesis to elucidate the significance of symmetry breaking in enhancing neural network optimization. We demonstrate that a simple input expansion can significantly improve network performance across various tasks, and we show that this improvement can be attributed to the underlying symmetry breaking mechanism. We further develop a metric to quantify the degree of symmetry breaking in neural networks, providing a practical approach to evaluate and guide network design. Our findings confirm that symmetry breaking is a fundamental principle that underpins various optimization techniques, including dropout, batch normalization, and equivariance. By quantifying the degree of symmetry breaking, our work offers a practical technique for performance enhancement and a metric to guide network design without the need for complete datasets and extensive training processes.

On the uncertainty principle of neural networks

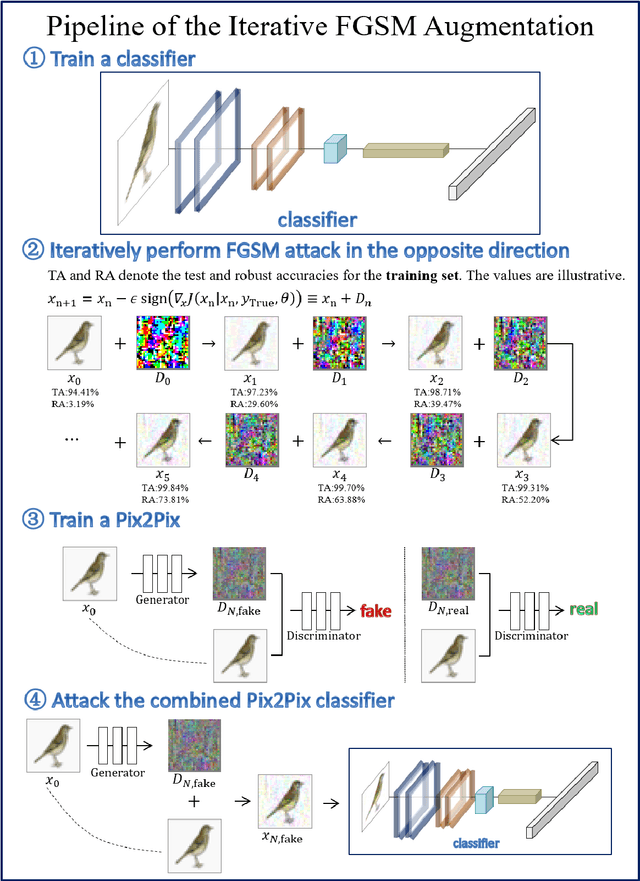
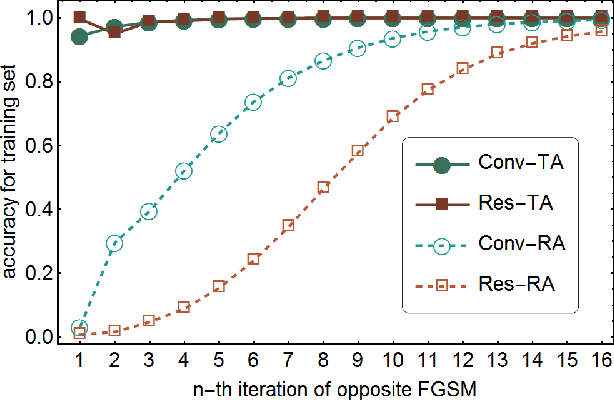
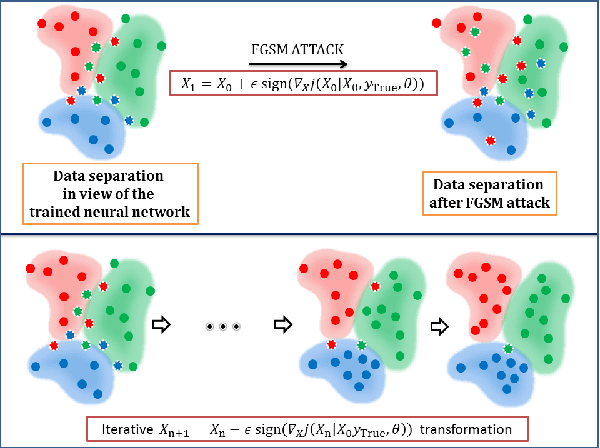
Despite the successes in many fields, it is found that neural networks are vulnerability and difficult to be both accurate and robust (robust means that the prediction of the trained network stays unchanged for inputs with non-random perturbations introduced by adversarial attacks). Various empirical and analytic studies have suggested that there is more or less a trade-off between the accuracy and robustness of neural networks. If the trade-off is inherent, applications based on the neural networks are vulnerable with untrustworthy predictions. It is then essential to ask whether the trade-off is an inherent property or not. Here, we show that the accuracy-robustness trade-off is an intrinsic property whose underlying mechanism is deeply related to the uncertainty principle in quantum mechanics. We find that for a neural network to be both accurate and robust, it needs to resolve the features of the two conjugated parts $x$ (the inputs) and $\Delta$ (the derivatives of the normalized loss function $J$ with respect to $x$), respectively. Analogous to the position-momentum conjugation in quantum mechanics, we show that the inputs and their conjugates cannot be resolved by a neural network simultaneously.