A Probabilistic Representation of DNNs: Bridging Mutual Information and Generalization

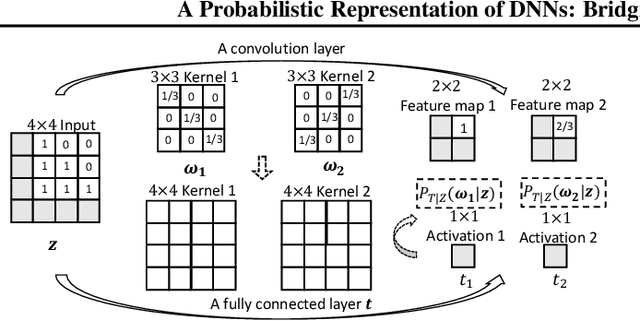
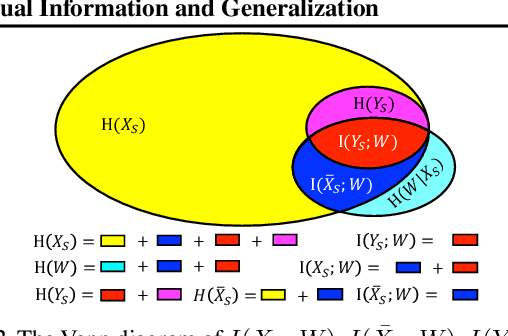
Recently, Mutual Information (MI) has attracted attention in bounding the generalization error of Deep Neural Networks (DNNs). However, it is intractable to accurately estimate the MI in DNNs, thus most previous works have to relax the MI bound, which in turn weakens the information theoretic explanation for generalization. To address the limitation, this paper introduces a probabilistic representation of DNNs for accurately estimating the MI. Leveraging the proposed MI estimator, we validate the information theoretic explanation for generalization, and derive a tighter generalization bound than the state-of-the-art relaxations.

A Probabilistic Representation of Deep Learning for Improving The Information Theoretic Interpretability

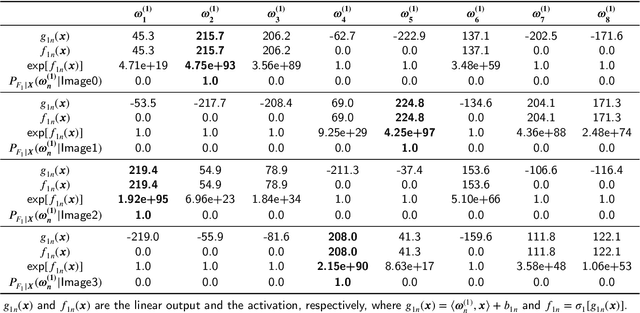
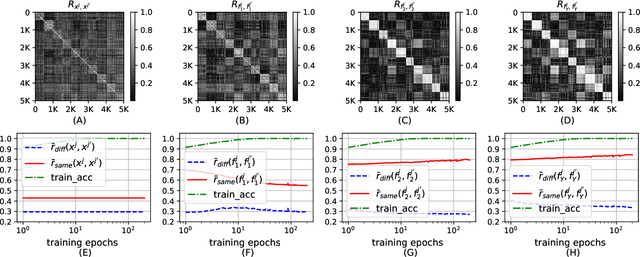
In this paper, we propose a probabilistic representation of MultiLayer Perceptrons (MLPs) to improve the information-theoretic interpretability. Above all, we demonstrate that the activations being i.i.d. is not valid for all the hidden layers of MLPs, thus the existing mutual information estimators based on non-parametric inference methods, e.g., empirical distributions and Kernel Density Estimate (KDE), are invalid for measuring the information flow in MLPs. Moreover, we introduce explicit probabilistic explanations for MLPs: (i) we define the probability space (Omega_F, t, P_F) for a fully connected layer f and demonstrate the great effect of an activation function on the probability measure P_F ; (ii) we prove the entire architecture of MLPs as a Gibbs distribution P; and (iii) the back-propagation aims to optimize the sample space Omega_F of all the fully connected layers of MLPs for learning an optimal Gibbs distribution P* to express the statistical connection between the input and the label. Based on the probabilistic explanations for MLPs, we improve the information-theoretic interpretability of MLPs in three aspects: (i) the random variable of f is discrete and the corresponding entropy is finite; (ii) the information bottleneck theory cannot correctly explain the information flow in MLPs if we take into account the back-propagation; and (iii) we propose novel information-theoretic explanations for the generalization of MLPs. Finally, we demonstrate the proposed probabilistic representation and information-theoretic explanations for MLPs in a synthetic dataset and benchmark datasets.

PAC-Bayesian Generalization Bounds for MultiLayer Perceptrons

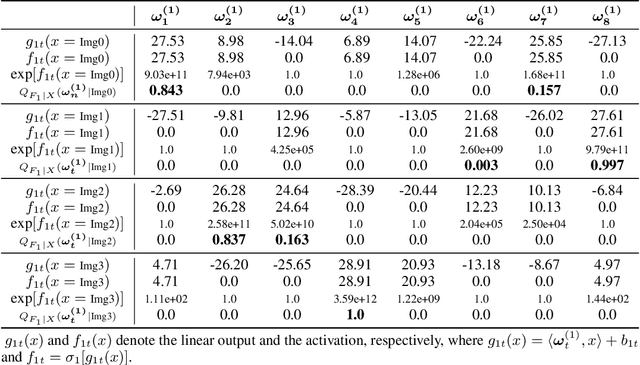
We study PAC-Bayesian generalization bounds for Multilayer Perceptrons (MLPs) with the cross entropy loss. Above all, we introduce probabilistic explanations for MLPs in two aspects: (i) MLPs formulate a family of Gibbs distributions, and (ii) minimizing the cross-entropy loss for MLPs is equivalent to Bayesian variational inference, which establish a solid probabilistic foundation for studying PAC-Bayesian bounds on MLPs. Furthermore, based on the Evidence Lower Bound (ELBO), we prove that MLPs with the cross entropy loss inherently guarantee PAC- Bayesian generalization bounds, and minimizing PAC-Bayesian generalization bounds for MLPs is equivalent to maximizing the ELBO. Finally, we validate the proposed PAC-Bayesian generalization bound on benchmark datasets.

Explicitly Bayesian Regularizations in Deep Learning

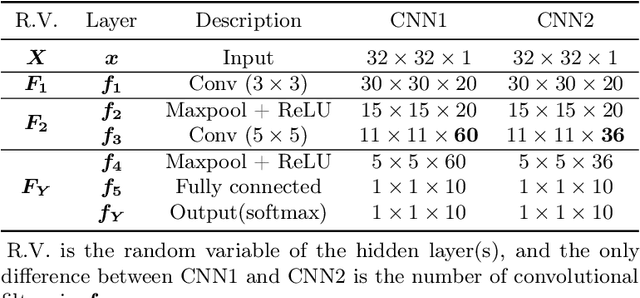
Generalization is essential for deep learning. In contrast to previous works claiming that Deep Neural Networks (DNNs) have an implicit regularization implemented by the stochastic gradient descent, we demonstrate explicitly Bayesian regularizations in a specific category of DNNs, i.e., Convolutional Neural Networks (CNNs). First, we introduce a novel probabilistic representation for the hidden layers of CNNs and demonstrate that CNNs correspond to Bayesian networks with the serial connection. Furthermore, we show that the hidden layers close to the input formulate prior distributions, thus CNNs have explicitly Bayesian regularizations based on the Bayesian regularization theory. In addition, we clarify two recently observed empirical phenomena that are inconsistent with traditional theories of generalization. Finally, we validate the proposed theory on a synthetic dataset

A Probabilistic Representation of Deep Learning

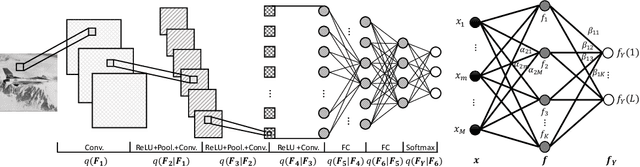
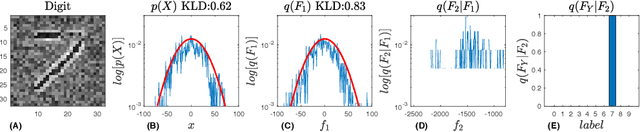
In this work, we introduce a novel probabilistic representation of deep learning, which provides an explicit explanation for the Deep Neural Networks (DNNs) in three aspects: (i) neurons define the energy of a Gibbs distribution; (ii) the hidden layers of DNNs formulate Gibbs distributions; and (iii) the whole architecture of DNNs can be interpreted as a Bayesian neural network. Based on the proposed probabilistic representation, we investigate two fundamental properties of deep learning: hierarchy and generalization. First, we explicitly formulate the hierarchy property from the Bayesian perspective, namely that some hidden layers formulate a prior distribution and the remaining layers formulate a likelihood distribution. Second, we demonstrate that DNNs have an explicit regularization by learning a prior distribution and the learning algorithm is one reason for decreasing the generalization ability of DNNs. Moreover, we clarify two empirical phenomena of DNNs that cannot be explained by traditional theories of generalization. Simulation results validate the proposed probabilistic representation and the insights into these properties of deep learning based on a synthetic dataset.