A Probabilistic Representation of Deep Learning
Paper and Code
Aug 26, 2019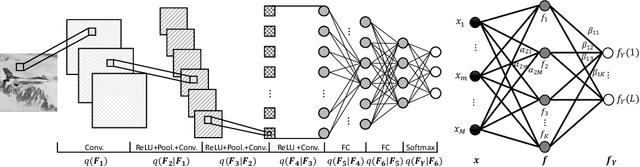
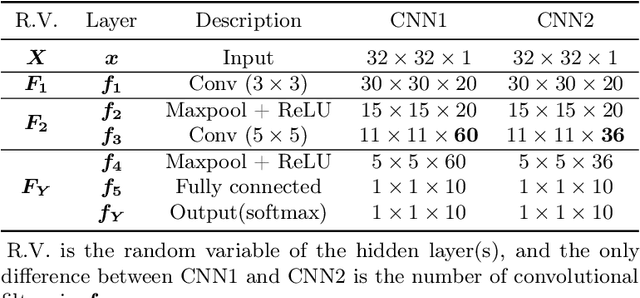

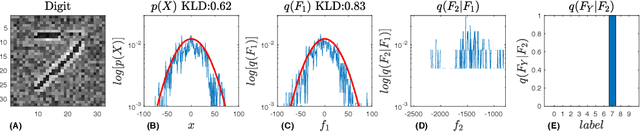
In this work, we introduce a novel probabilistic representation of deep learning, which provides an explicit explanation for the Deep Neural Networks (DNNs) in three aspects: (i) neurons define the energy of a Gibbs distribution; (ii) the hidden layers of DNNs formulate Gibbs distributions; and (iii) the whole architecture of DNNs can be interpreted as a Bayesian neural network. Based on the proposed probabilistic representation, we investigate two fundamental properties of deep learning: hierarchy and generalization. First, we explicitly formulate the hierarchy property from the Bayesian perspective, namely that some hidden layers formulate a prior distribution and the remaining layers formulate a likelihood distribution. Second, we demonstrate that DNNs have an explicit regularization by learning a prior distribution and the learning algorithm is one reason for decreasing the generalization ability of DNNs. Moreover, we clarify two empirical phenomena of DNNs that cannot be explained by traditional theories of generalization. Simulation results validate the proposed probabilistic representation and the insights into these properties of deep learning based on a synthetic dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge