PAC-Bayesian Generalization Bounds for MultiLayer Perceptrons

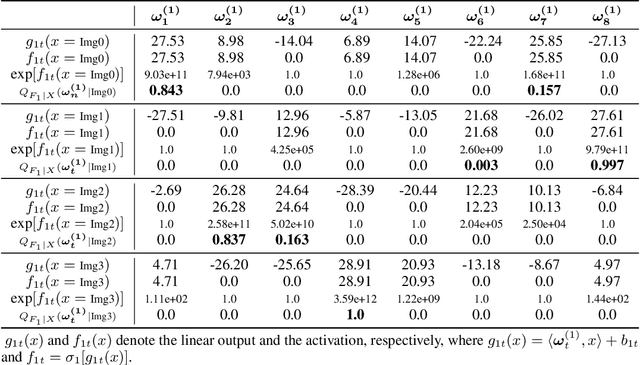
We study PAC-Bayesian generalization bounds for Multilayer Perceptrons (MLPs) with the cross entropy loss. Above all, we introduce probabilistic explanations for MLPs in two aspects: (i) MLPs formulate a family of Gibbs distributions, and (ii) minimizing the cross-entropy loss for MLPs is equivalent to Bayesian variational inference, which establish a solid probabilistic foundation for studying PAC-Bayesian bounds on MLPs. Furthermore, based on the Evidence Lower Bound (ELBO), we prove that MLPs with the cross entropy loss inherently guarantee PAC- Bayesian generalization bounds, and minimizing PAC-Bayesian generalization bounds for MLPs is equivalent to maximizing the ELBO. Finally, we validate the proposed PAC-Bayesian generalization bound on benchmark datasets.