A Probabilistic Representation of Deep Learning for Improving The Information Theoretic Interpretability
Paper and Code
Oct 27, 2020
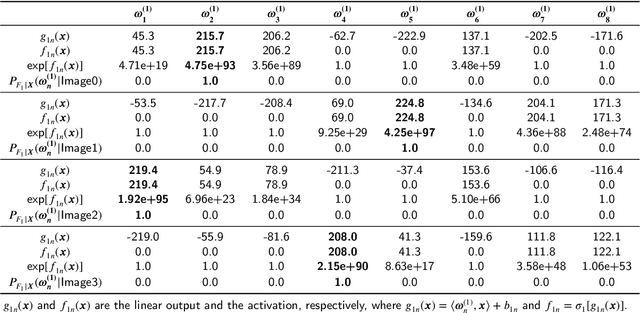
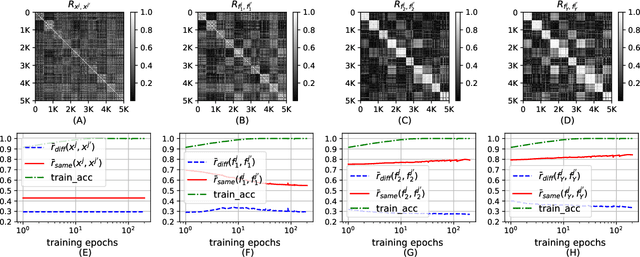

In this paper, we propose a probabilistic representation of MultiLayer Perceptrons (MLPs) to improve the information-theoretic interpretability. Above all, we demonstrate that the activations being i.i.d. is not valid for all the hidden layers of MLPs, thus the existing mutual information estimators based on non-parametric inference methods, e.g., empirical distributions and Kernel Density Estimate (KDE), are invalid for measuring the information flow in MLPs. Moreover, we introduce explicit probabilistic explanations for MLPs: (i) we define the probability space (Omega_F, t, P_F) for a fully connected layer f and demonstrate the great effect of an activation function on the probability measure P_F ; (ii) we prove the entire architecture of MLPs as a Gibbs distribution P; and (iii) the back-propagation aims to optimize the sample space Omega_F of all the fully connected layers of MLPs for learning an optimal Gibbs distribution P* to express the statistical connection between the input and the label. Based on the probabilistic explanations for MLPs, we improve the information-theoretic interpretability of MLPs in three aspects: (i) the random variable of f is discrete and the corresponding entropy is finite; (ii) the information bottleneck theory cannot correctly explain the information flow in MLPs if we take into account the back-propagation; and (iii) we propose novel information-theoretic explanations for the generalization of MLPs. Finally, we demonstrate the proposed probabilistic representation and information-theoretic explanations for MLPs in a synthetic dataset and benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge