Xinhao Yi
A Comprehensive Survey of Self-Evolving AI Agents: A New Paradigm Bridging Foundation Models and Lifelong Agentic Systems
Aug 10, 2025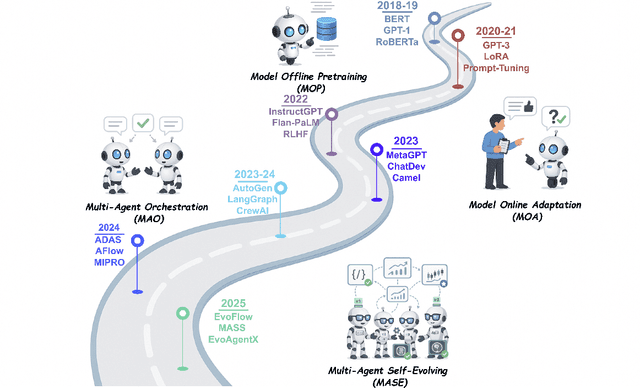
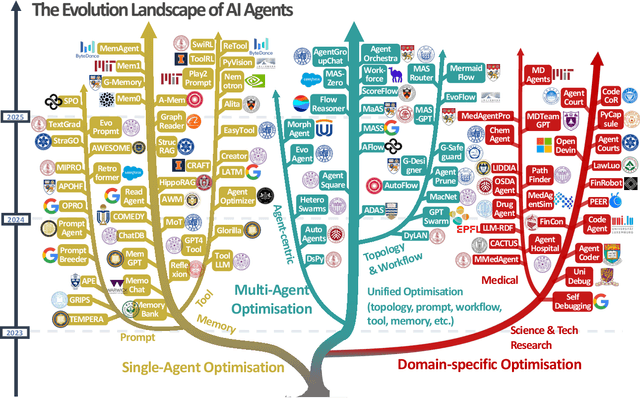
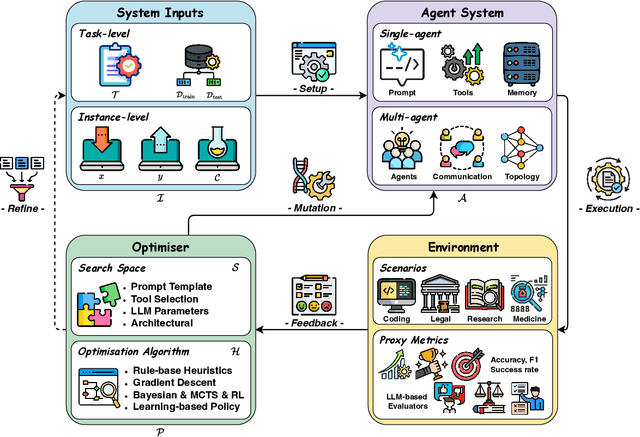
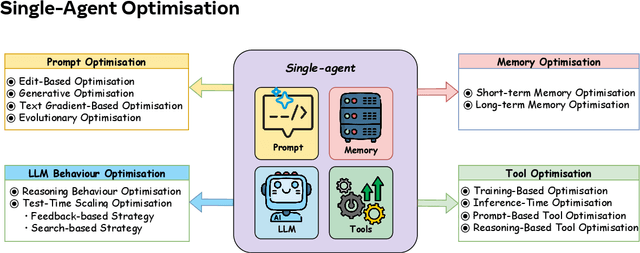
Abstract:Recent advances in large language models have sparked growing interest in AI agents capable of solving complex, real-world tasks. However, most existing agent systems rely on manually crafted configurations that remain static after deployment, limiting their ability to adapt to dynamic and evolving environments. To this end, recent research has explored agent evolution techniques that aim to automatically enhance agent systems based on interaction data and environmental feedback. This emerging direction lays the foundation for self-evolving AI agents, which bridge the static capabilities of foundation models with the continuous adaptability required by lifelong agentic systems. In this survey, we provide a comprehensive review of existing techniques for self-evolving agentic systems. Specifically, we first introduce a unified conceptual framework that abstracts the feedback loop underlying the design of self-evolving agentic systems. The framework highlights four key components: System Inputs, Agent System, Environment, and Optimisers, serving as a foundation for understanding and comparing different strategies. Based on this framework, we systematically review a wide range of self-evolving techniques that target different components of the agent system. We also investigate domain-specific evolution strategies developed for specialised fields such as biomedicine, programming, and finance, where optimisation objectives are tightly coupled with domain constraints. In addition, we provide a dedicated discussion on the evaluation, safety, and ethical considerations for self-evolving agentic systems, which are critical to ensuring their effectiveness and reliability. This survey aims to provide researchers and practitioners with a systematic understanding of self-evolving AI agents, laying the foundation for the development of more adaptive, autonomous, and lifelong agentic systems.
Can We Edit LLMs for Long-Tail Biomedical Knowledge?
Apr 14, 2025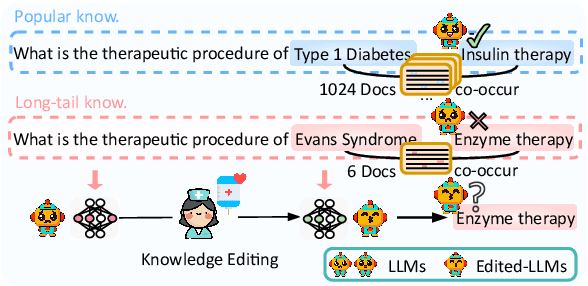
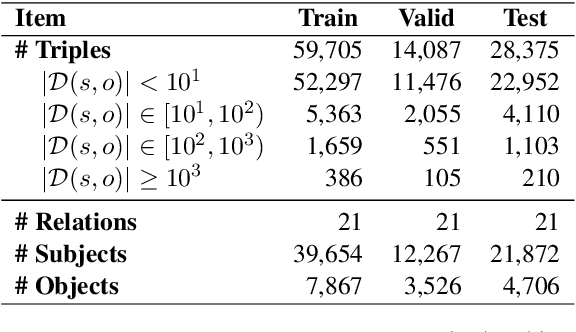
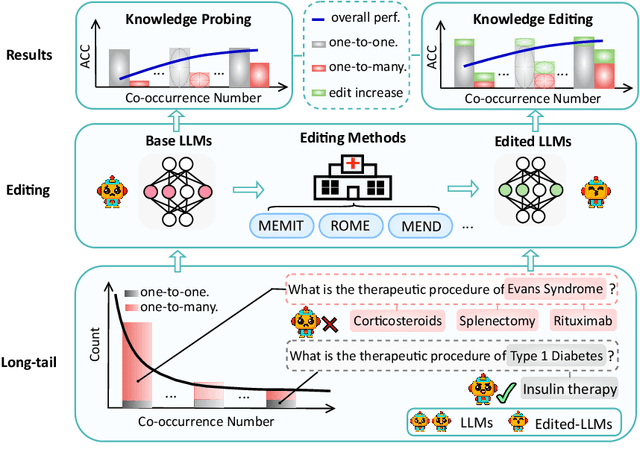
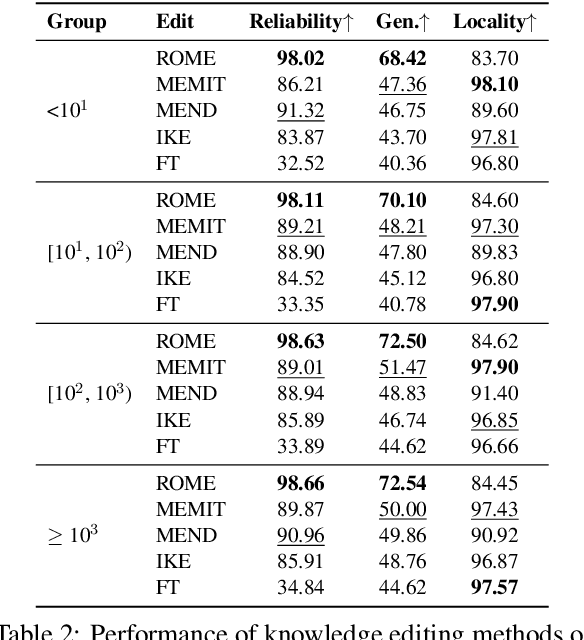
Abstract:Knowledge editing has emerged as an effective approach for updating large language models (LLMs) by modifying their internal knowledge. However, their application to the biomedical domain faces unique challenges due to the long-tailed distribution of biomedical knowledge, where rare and infrequent information is prevalent. In this paper, we conduct the first comprehensive study to investigate the effectiveness of knowledge editing methods for editing long-tail biomedical knowledge. Our results indicate that, while existing editing methods can enhance LLMs' performance on long-tail biomedical knowledge, their performance on long-tail knowledge remains inferior to that on high-frequency popular knowledge, even after editing. Our further analysis reveals that long-tail biomedical knowledge contains a significant amount of one-to-many knowledge, where one subject and relation link to multiple objects. This high prevalence of one-to-many knowledge limits the effectiveness of knowledge editing in improving LLMs' understanding of long-tail biomedical knowledge, highlighting the need for tailored strategies to bridge this performance gap.
DuSEGO: Dual Second-order Equivariant Graph Ordinary Differential Equation
Nov 15, 2024
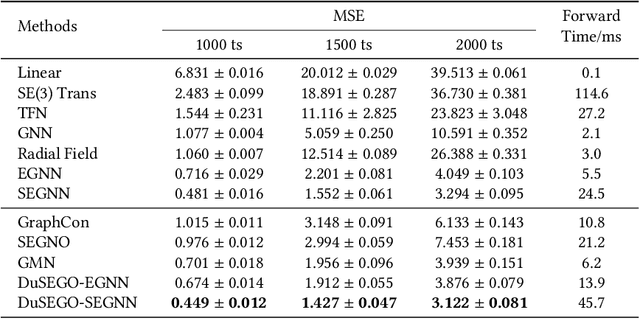
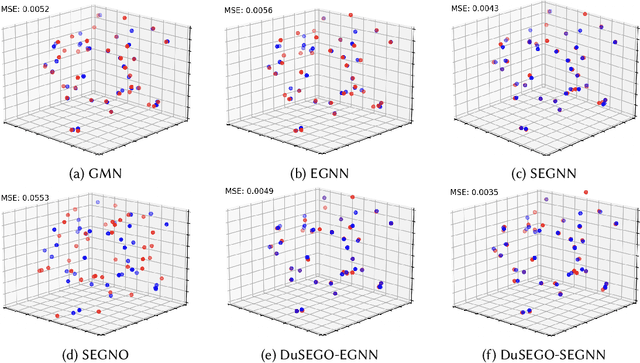
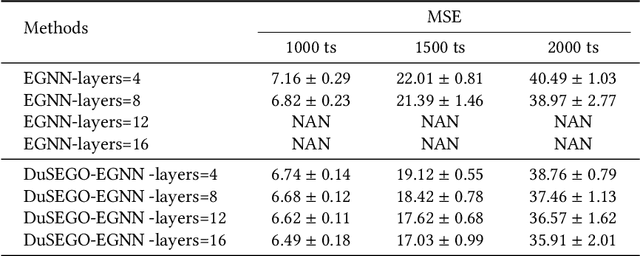
Abstract:Graph Neural Networks (GNNs) with equivariant properties have achieved significant success in modeling complex dynamic systems and molecular properties. However, their expressiveness ability is limited by: (1) Existing methods often overlook the over-smoothing issue caused by traditional GNN models, as well as the gradient explosion or vanishing problems in deep GNNs. (2) Most models operate on first-order information, neglecting that the real world often consists of second-order systems, which further limits the model's representation capabilities. To address these issues, we propose the \textbf{Du}al \textbf{S}econd-order \textbf{E}quivariant \textbf{G}raph \textbf{O}rdinary Differential Equation (\method{}) for equivariant representation. Specifically, \method{} apply the dual second-order equivariant graph ordinary differential equations (Graph ODEs) on graph embeddings and node coordinates, simultaneously. Theoretically, we first prove that \method{} maintains the equivariant property. Furthermore, we provide theoretical insights showing that \method{} effectively alleviates the over-smoothing problem in both feature representation and coordinate update. Additionally, we demonstrate that the proposed \method{} mitigates the exploding and vanishing gradients problem, facilitating the training of deep multi-layer GNNs. Extensive experiments on benchmark datasets validate the superiority of the proposed \method{} compared to baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge